Tasa de Variación Instantánea

La tasa de variación instantánea de una función en un punto nos dice cuánto varía la función en dicho punto, es decir, cuál es su crecimiento. Para profundizar en esta idea estudiaremos los siguientes puntos:

• Concepto
• Expresión
• Interpretación geométrica
• Relación con la derivada

Para entender la tasa de variación instantánea es importante que estés familiarizado con la idea de tasa de variación media en un intervalo. Por otro lado, a partir de la tasa de variación instantánea podrás entender claramente qué es la derivada de una función.

¿Empezamos?

Concepto

Observa la siguiente imagen:

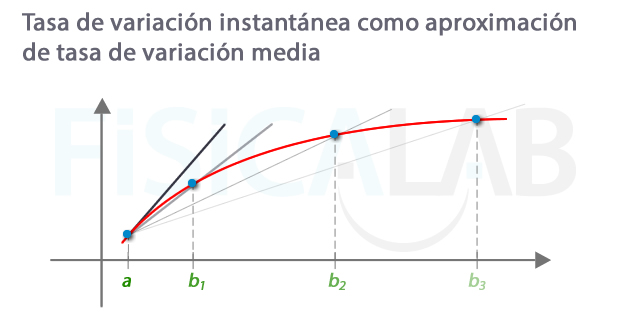
Concepto de tasa de variación instantánea

Si queremos conocer la variación de la función en un punto a podemos comenzar buscando la variación media en un intervalo, por ejemplo (a, b), y haciendo este cada vez  más pequeño, aproximando b a a. En la ilustración puedes ver la recta secante que representa la tasa de variación media en intervalos cada vez más pequeños, (a, b₃), (a,b₂) y (a,b₁). Si conseguimos aproximarnos lo suficiente, llegaríamos a la recta negra, tangente a la función en a.

Recuerda que la tasa de variación media nos daba el crecimiento en un intervalo, por tanto, haciendo el intervalo infinitamente pequeño obtenemos la variación o rapidez de cambio en el punto, que es precisamente lo que andábamos buscando.

Expresión

Comprobación

Puedes verificar que ambas expresiones son equivalentes, haciendo b=a+h. De esta manera:

$$b\to a\underset{b=a+h}{\Rightarrow }h\to 0$$

Por otro lado:

$$\frac{f\left(b\right)-f\left(a\right)}{b-a}\underset{b=a+h}{=}\frac{f\left(a+h\right)-f\left(a\right)}{a+h-a}=\hspace{0.17em}\frac{f\left(a+h\right)-f\left(a\right)}{h}$$

Con lo que...

$$T.V.I.\left(a\right) =\underset{b\to a}{\lim }\frac{f\left(b\right)-f\left(a\right)}{b-a}=\underset{h\to 0}{\lim }\hspace{0.17em}\frac{f\left(a+h\right)-f\left(a\right)}{h}$$

Interpretación geométrica

Geométricamente, la tasa de variación instantánea en el punto a es la pendiente de la recta tangente a la función en dicho punto:

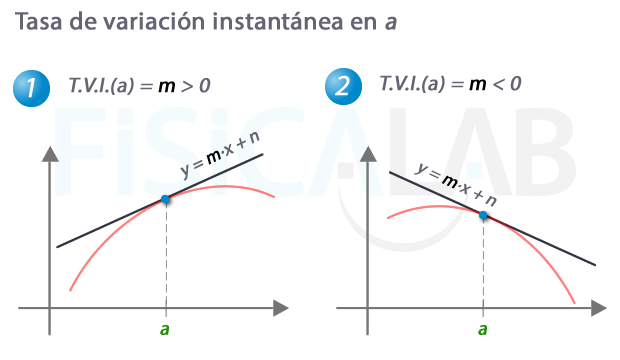
Representación gráfica de la tasa de variación instantánea

En negro, la recta tangente a la función en el punto de abscisa a. El valor de su pendiente, m, es, precisamente, la tasa de variación instantánea. Observa que, en 1, la función es creciente en el punto considerado, siendo T.V.I. > 0. En cambio, en 2, la función es decreciente y la T.V.I. < 0.

Relación con la derivada

A la tasa de variación instantánea de la función, en el punto a, también se le denomina derivada de la función en el punto a, y es designada f'(a). Por otro lado, podemos generalizar esta idea para cualquier valor genérico de x. Así, dada una función cualquiera f(x), se conoce como función derivada de esta a aquella función que hace corresponder cada valor de x con el valor de la derivada de la función en ese x concreto, es decir, con el valor de la tasa de variación instantánea de f en ese punto. Matemáticamente no hay más que cambiar a por x en la definición de f'(a):

$$f\text{'}\left(a\right)=\underset{h\to 0}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}\Rightarrow f\text{'}\left(x\right)=\underset{h\to 0}{\lim }\frac{f\left(x+h\right)-f\left(x\right)}{h}$$

Profundizaremos sobre esta idea y su interpretación en física en el apartado dedicado a la función derivada.