Números Complejos

Unidad Imaginaria

Cuando hayas intentado resolver ciertas ecuaciones te habrás dado cuenta de que en ocasiones no es posible encontrar una solución real, es decir, no existe ningún número real ℝ que sea solución de dichas ecuaciones.

Por ejemplo, si intentamos resolver la siguiente ecuación $x^2+25 = 0$ nos damos cuenta de que $x=\pm \sqrt{-25}$, sin embargo $\sqrt{-25}$ es una operación "imposible" ya que no existe ningún número real que elevado al cuadrado nos de como resultado -25.

Con el fin de que todos los números posean raíz cuadrada, se amplía el conjunto formado por los números reales ℝ creando un nuevo conjunto denominado números complejos (ℂ), de tal forma que ℝ es un subconjunto de ℂ (ℝ⊂ℂ).

En este nuevo conjunto numérico aparece un número especial denominado unidad imaginaria (i) que representa a la raíz de -1.

De esta forma, nuestra ecuación anterior $x^2+25 = 0$  tiene dos soluciones:

$$\begin{gathered} x=\pm \sqrt{-25} \Rightarrow x=\pm \sqrt{25}·\sqrt{-1}\Rightarrow x=\pm 5·i \\ \underline{x=5i} y \underline{x=-5i} \end{gathered}$$

Potencias de la Unidad Imaginaria

El cálculo de cualquier potencia de la unidad imaginaria se puede realizar por medio de un sencillo procedimiento. Para ello es necesario conocer de antemano las cuatro primeras potencias de i:

$$\begin{gathered} i^0 = 1 \\ {i}^1=i \\ {i}^2=(\sqrt{-1}{)}^2\hspace{0.17em}=\hspace{0.17em}-1 \\ {i}^3=i^2·i = -1 ·i = -i \end{gathered}$$

Ya que el valor de i elevado a cualquier número n es:

$$i^n = i{ }^{n \text{mod 4}}$$

donde:

• mod es la operación de obtener el resto al dividir n entre 4.
• El resultado de esa operación siempre nos dará un número entre 0 y 3, lo que implica que cualquier potencia de i se reduce a conocer el valor de i⁰, i¹, i² e i³.

Ejemplo.

$$i^7 = i{ }^{7 \text{mod 4}} = i^3 = -i$$

Números Complejos en Forma binómica

Siempre que resuelvas una ecuación de segundo grado cuyo discriminante sea negativo, obtendrás una solución de la forma a+bi o simplemente bi. Recuerda que el discriminante (Δ) de una ecuación de segundo grado ax²+bx+c=0 es Δ=b²-4ac.

Por todo lo comentado anteriormente, podemos decir que son números complejos todos los mostrados a continuación:

$$3+4i, 5i, 3, -7i, 1-2i, 0, ...$$

En concreto, aquellos número complejos cuya parte real sea nula (por ejemplo, 3i) reciben adicionalmente el nombre de números imaginarios.

Números Complejos en Forma Polar

Cada número complejo en forma binómica a + bi se puede representar como un punto P(a,b) en un plano denominado plano complejo. De esta forma, la parte real se puede representar en el eje de abcisas, también denominado eje real y la parte imaginaria en el eje de ordenadas, también llamado eje imaginario. 

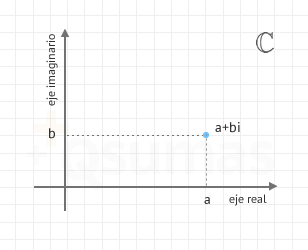
Representación de los números complejos

A cada número complejo a+bi le corresponde un punto en un plano. Dicho punto posee las coordenadas (a,b). 

Como podrás suponer esta no es la única forma de representarlo. De hecho, otra forma alternativa de representación consiste en utilizar el vector  que se define entre el origen de coordenadas y el punto P (denominado afijo del número complejo). De esta forma cada número complejo en vez de venir determinado únicamente por los valores a y b puede venir dado por la longitud (o módulo) del vector  y el ángulo α (o argumento) que se forma entre el vector y el semieje positivo real.

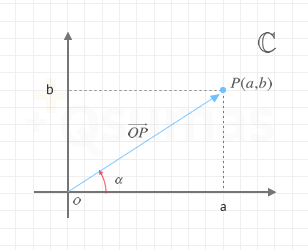
Representación de números complejos en forma polar

Cualquier número complejo a+bi está representado por su afijo en las coordenadas (a,b). Dicho punto puede venir dado igualmente por la longitud del vector que une el origen con el afijo ($\overrightarrow{OP}$) y ángulo (α) que forma con el semieje positivo de abscisas.

De esta forma podemos encontrar número complejos representados en forma polar tales como:

$$2_{30º}, {15}_{90º},{\left(5\sqrt{2}\right)}_{315º}, ...$$