Ejercicio completo de primera ley de la termodinámica

Enunciado

dificultad

Se sitúan 15 L de gas ideal en un recipiente a 27 ºC. El recipiente cuenta con un pistón móvil libre de rozamiento. La presión en el exterior se mantiene constante a 750 mmHg. Determina, si se eleva la temperatura a 190 ºC:

El trabajo realizado en el proceso
La variación de energía interna que tiene lugar
El calor transferido durante el mismo
Representa el proceso en un diagrama presión - volumen ( p - V )

Datos : c_v = 5·R/2 ; R = 8.31 J/ mol·K

Solución

Datos

Volumen inicial V_i = 15 L = 15·10^-3 m³
Temperatura inicial T_i = 27 ºC = 300.15 K
Temperatura final T_f = 190 ºC = 463.15 K
Presión constante p = 750 mmHg = 750·101325/760 = 99991.77 Pa
Calor específico a volumen constante c_v = 5·R/2
Constante universal de los gases ideales R = 8.31 J/ mol·K

Consideraciones previas

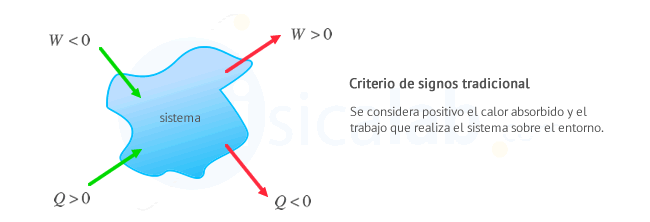
Usaremos el criterio de signos tradicional según el cual el trabajo es positivo se realiza contra el exterior

Resolución

En los procesos a presión constante el trabajo termodinámico, según el criterio de signos establecido, viene dado por la expresión:

$W = p \cdot ∆ V = p \cdot (V_{f} - V_{i})$

Para determinar el volumen final podemos aplicar la ecuación de estado de los gases ideales, de la siguiente manera:

$\begin{array}{r} p \cdot V_{i} = n \cdot R \cdot T_{i} \\ p \cdot V_{f} = n \cdot R \cdot T_{f} \end{array}\} \begin{array}{r} p = \frac{n \cdot R \cdot T_{i}}{V_{i}} \\ p = \frac{n \cdot R \cdot T_{f}}{V_{f}} \end{array}\} \frac{n \cdot R \cdot T_{i}}{V_{i}} = \frac{n \cdot R \cdot T_{f}}{V_{f}} \Rightarrow \frac{V_{i}}{T_{i}} = \frac{V_{f}}{T_{f}}$

La expresión anterior constituye la ley de Charles y Gay-Lussac. A partir de ella, nos queda:

$\frac{V_{i}}{T_{i}} = \frac{V_{f}}{T_{f}} \Rightarrow V_{f} = \frac{V_{i}}{T_{i}} \cdot T_{f} = \frac{15 \cdot 10^{- 3}}{300.15} \cdot 463.15 = 23.14 \cdot 10^{- 3} m^{3}$

Y volviendo a la expresión del trabajo termodinámico nos queda:

$W = p \cdot (V_{f} - V_{i}) = 99991.77 \cdot (23.14 - 15) \cdot 10^{- 3} = 813.93 J$

Presta atención a este apartado por que vamos a utilizar una serie de conceptos que debes tener claros. En primer lugar, la variación de energía interna en un gas depende únicamente de la variación de temperatura. En el diagrama p - V de la figura puedes ver representadas las dos isotermas características del proceso.

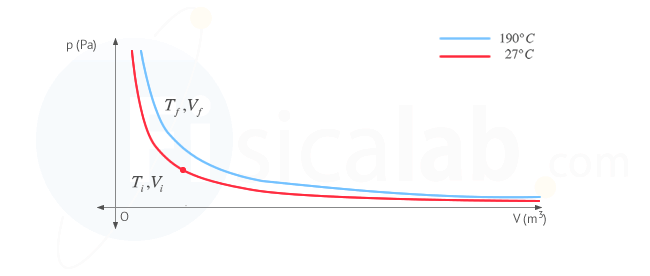
Isoterma en rojo: es la de aquellos puntos genéricos ( V, p) que se corresponden con una temperatura de 27 ºC. A todos ellos les corresponde una determinada energía interna del sistema
Isoterma en azul: es la de aquellos puntos genéricos ( V, p) que se corresponden con una temperatura de 190 ºC. A todos ellos les corresponde una determinada energía interna del sistema

En el proceso, al variar la temperatura varía la energía interna, es decir, nos desplazamos de una isoterma a otra realizando un determinado trabajo y transfiriendo un determinado calor. Independientemente de la forma en que nos desplacemos de una isoterma a otra (esto es, la cantidad de calor y trabajo que intervenga en el proceso), la variación de energía interna dependerá unicamente de la isoterma inicial y la isoterma final. Es por ello que, dado que nos dan como dato c_v(calor específico a volumen constante), estudiaremos la variación de energía interna suponiendo un proceso isocórico ( a volumen constante ) donde el volumen no cambia y, por tanto, el desplazamiento de una isoterma a otra se realizaría exclusivamente mediante el intercambio de calor, al ser el trabajo realizado cero ( W = 0 ) . De esta forma, nos queda:

$∆ U = Q - W$

Por otro lado, dado que nos dan c_v referida a cantidad de sustancia ( mol ), utilizaremos, para el cálculo del calor, la expresión:

$Q = n \cdot c_{v} \cdot ∆ T$

Observa que ya habíamos presentado en teoría dicha expresión al hablar de la variación de energía interna de un gas cuando se incrementa la temperatura.

Para el cálculo de n aplicamos de nuevo la ecuación de estado de los gases ideales:

$p \cdot V_{i} = n \cdot R \cdot T_{i} \Rightarrow n = \frac{p \cdot V_{i}}{R \cdot T_{i}} = \frac{99991.77 \cdot 15 \cdot 10^{- 3}}{8.31 \cdot 300.15} = 0.6 mol$

Finalmente, volviendo a la ecuación de la variación de energía interna en un proceso isocórico, tenemos:

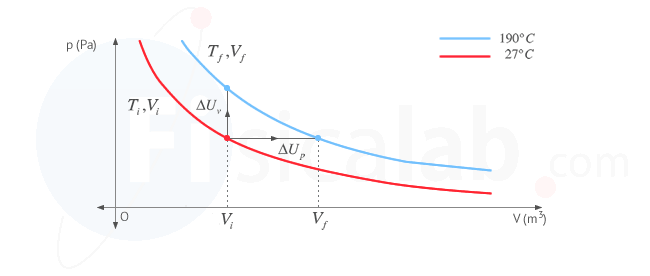
$∆ U = Q = n \cdot c_{v} \cdot ∆ T = 0.6 \cdot \frac{5 \cdot 8.31}{2} \cdot 163 = 2031.795 J$

En la siguiente figura se representa el proceso que tendría lugar a volumen constante y que nos sirve para determinar la variación de energía interna también en nuestro proceso a presión constante.

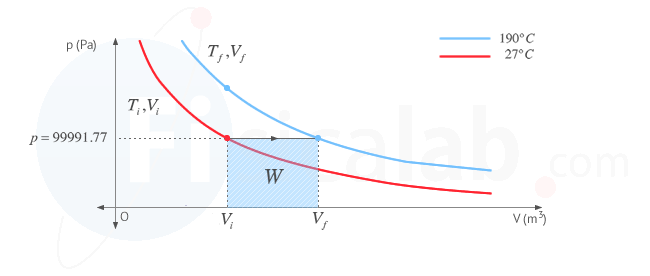
Podemos aplicar la primera ley de la termodinámica para determinar el calor transferido en el proceso. Ten en cuenta que, tal y como hemos dicho en el punto 2, la variación de energía interna es igual a la que se experimenta en el proceso a volumen constante ya que las temperaturas inicial y final son las mismas:

$∆ U = Q - W \Rightarrow Q = ∆ U + W = 2031.795 + 813.93 = 2845.725 J$

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Fórmulas

Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.

Fórmulas

Apartados relacionados