Posición
Existen dos conceptos clave para describir los movmientos de los cuerpos: el lugar en el que se encuentra el cuerpo ó, dicho de otra forma, su posición y el momento en el que se encuentra en ese lugar ó, dicho de otro modo, el instante de tiempo. Vamos a explicar esos dos conceptos.
Instante
El instante de tiempo es uno de los parámetros usados para describir los movimientos en Física. Se representa por la letra t, en ocasiones acompañada por uno o varios subíndices que pueden indicar el lugar que ocupa el dato en un conjunto de medidas. Por ejemplo, para denotar dos instantes de tiempo consecutivos se puede utilizar los subíndice 1 y 2, quedando la representación de los mismos como t1 y t2. En otras ocasiones para indicar un instante inicial y otro final se puede indicar por ti y tf respectivamente. Su unidad de medida en el Sistema Internacional (S.I.) es el segundo [s].
Para indicar el tiempo transcurrido entre dos instantes concretos se suele usar
Imagina que obtienes una serie de datos por la lectura directa del cronómetro de tu teléfono móvil: 0s, 5 s, 10 s, 15 s, 20 s. Estos datos podrían representarse de la siguiente forma en una tabla:
| Situación | Símbolo y valor | Tiempo transcurrido |
|---|---|---|
| Inicio | t0 = 0 s | |
| 1 | t1 = 5 s | |
| 2 | t2 = 10 s | |
| 3 | t3 = 15 s | |
| 4 | t4 = 20 s |
Posición
Para determinar la posición de un cuerpo primero establecemos el sistema de referencia. En un plano, en dos dimensiones, la coordenada X corresponde al eje de abcisa, eje horizontal y la coordenada Y al eje de ordenada, eje vertical. El observador se sitúa en el origen del Sistema de referencia (SR) y mediante un aparato de medida adecuado o a través de relaciones matemáticas, se determina el valor de cada posición (X,Y). Ese par, (X,Y), son las coordenadas del vector posición, ó simplemente posición, que une el punto en el que se encuentra el cuerpo con el origen de coordenadas.
En Física, la posición o vector de posición de un cuerpo respecto a un sistema de referencia se define como el vector que une el lugar ocupado por el cuerpo con el origen del sistema de referencia.
La unidad de medida en el Sistema Internacional es el metro [m]. Si conoces la posición de un cuerpo en cada instante de tiempo, el movimiento del mismo queda perfectamente descrito.
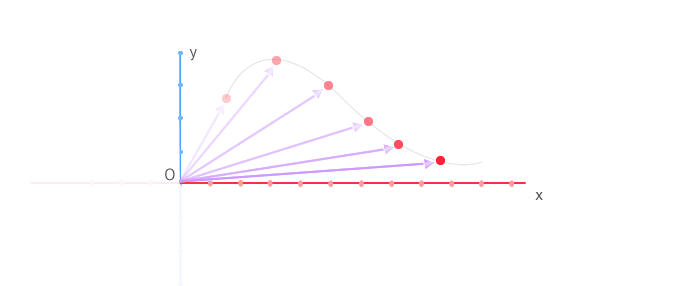
El vector posición, como todo vector, cuenta con un módulo, una dirección y un sentido.

-
Módulo: Su expresión viene dada por:
Representa la distancia al origen de coordenadas. Gráficamente se corresponde con el tamaño del vector. El vector se corresponde con la hipotenusa de un triángulo rectángulo que tiene como catetos las coordenadas X e Y. De ahí que podamos usar el teorema de Pitágoras para su cálculo. -
Dirección: Se trata de la recta que contiene al vector.
-
Sentido: El sentido, marcado por la punta de la flecha, apuntando al objeto en movimiento.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:
