Velocidad
El concepto cotidiano de velocidad surge cuando apreciamos la rapidez o lentitud con que se mueve un cuerpo. De alguna manera relacionamos el desplazamiento realizado con el tiempo invertido en él.
En este tema de introducción al movimiento para el nivel intermedio, vamos a estudiar dos magnitudes relacionadas con el concepto cotidiano de velocidad: la celeridad o rapidez y la velocidad. En este apartado abordamos el estudio de la velocidad de una forma sencilla que te permita entender con claridad este concepto en niveles más avanzados. Esto nos servirá para tener una primera aproximación de qué se entiende en Física por velocidad. Si necesitas información más precisa no dudes en consultar otros niveles más avanzados.
Concepto de Velocidad
El concepto de velocidad está asociado al cambio de posición de un cuerpo a lo largo del tiempo. Cuando necesitamos información sobre la dirección y el sentido del movimiento, así como su rapidez recurrimos a la velocidad.
La velocidad es una magnitud vectorial y, como tal, se representa mediante flechas que indican la dirección y sentido del movimiento que sigue un cuerpo y cuya longitud representa el valor numérico o módulo de la misma. Depende de el desplazamiento, es decir, de los puntos inicial y final del movimiento, y no como la rapidez, que depende directamente de la trayectoria.
Su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo (m/s), esto quiere decir que cuando por ejemplo afirmamos que la velocidad (módulo) de un cuerpo es de 5 metros por segundo (m/s), estamos indicando que cada segundo ese mismo cuerpo se desplaza 5 metros.
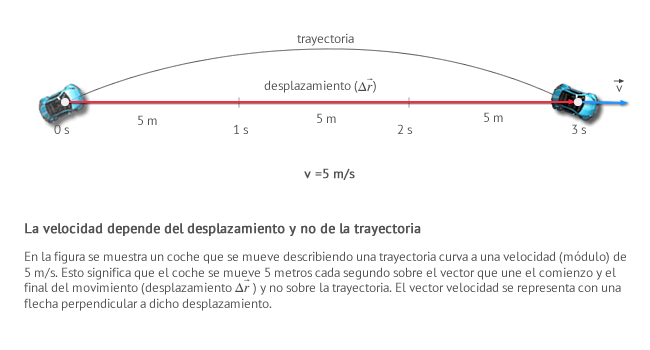
La velocidad puede definirse como la cantidad de espacio recorrido por unidad de tiempo con la que un cuerpo se desplaza en una determinada dirección y sentido. Se trata de un vector cuyo módulo, su valor numérico, se puede calcular mediante la expresión:
Donde:
- v: Módulo de la velocidad del cuerpo. Su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo (m/s)
- ∆r: Módulo del desplazamiento. Su unidad de medida en el Sistema Internacional (S.I.) es el metro (m)
- ∆t: Tiempo empleado en realizar el movimiento. Su unidad de medida en el Sistema Internacional (S.I.) es el segundo (s)
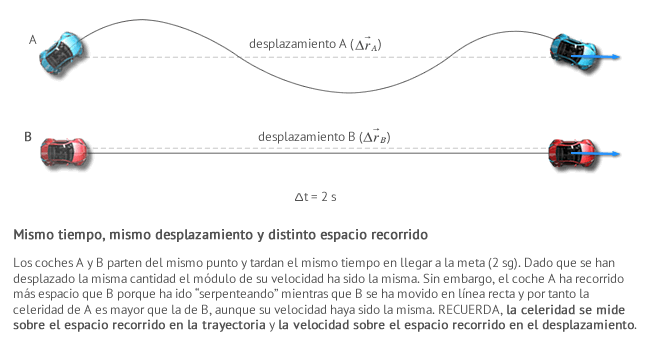
En el caso de los coches de la figura anterior, por ejemplo, parten y llegan a la vez a la meta. Aunque la velocidad de los dos es la misma (concepto vectorial de la velocidad), A ha recorrido mayor espacio en el mismo tiempo y, por tanto, su celeridad es mayor que B.
Otro aspecto de la velocidad es que un cuerpo que varía la dirección de su movimiento no mantiene constante la velocidad, ya que esta tiene en cuenta la dirección del mismo. Esto sucede aunque el módulo de la velocidad no cambie. Estudiaremos con más profundidad este aspecto en niveles más avanzados.
Aclaraciones
En este tema de introducción al movimiento y en este nivel educativo:
- Trabajamos con la velocidad en un intervalo de tiempo (entre dos instantes de tiempo), o velocidad media. Aunque existe la velocidad instantánea, la velocidad que tiene un cuerpo en un instante determinado de tiempo, su estudio lo abordaremos en niveles más avanzados.
- El módulo de la velocidad media es igual a la celeridad media o rapidez media cuando la trayectoria es una línea recta y no se produce cambio de sentido. En estos casos, y aunque el módulo de un vector es siempre una cantidad positiva, solemos adoptar, para facilitar cálculos, el siguiente convenio de signos:
- v>0: El móvil se mueve en el sentido positivo del eje
- v<0:El móvil se mueve en el sentido negativo del eje
- Con lo dicho hasta ahora, en los ejercicios de este nivel es frecuente que te encuentres el término velocidad referido a la celeridad media.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:
