Errores Absolutos y Relativos

Errores en la medición

Lo creas o no, cada vez que medimos tenemos una gran probabilidad de cometer algún tipo de error que nos ofrezca un resultado mas o menos alejado del que realmente deberíamos obtener. Y es que medir, es más bien un proceso aproximado que exacto. De entre los errores más comunes podemos distinguir dos grandes grupos:

• Errores sistemáticos. Son errores relacionados con la forma en la que su utiliza el instrumento de medida. Dentro de estos podemos distinguir otros como el error de calibrado o el error de paralaje.
  • Error de calibrado. Se trata de uno de los errores más frecuentes y está ligado directamente al instrumento. Muchos de ellos deben ser configurados de forma apropiada antes de ser utilizados (calibrado), si esto no se hace correctamente todas las medidas realizadas tendrán añadidas un sesgo.
  • Error de paralaje. Es propio de instrumentos de medida analógicos como por ejemplo aquellos que poseen agujas para marcar los valores. Dos observadores situados en posiciones oblicuas a la aguja pueden leer valores diferentes.
• Errores aleatorios o accidentales. Se tratan de errores que se producen debido a causas que no se pueden controlar. Para intentar reducir el efecto de este tipo de errores se suele medir varias veces en las mismas condiciones y se considera como valor final más probable la media aritmética de los datos obtenidos.

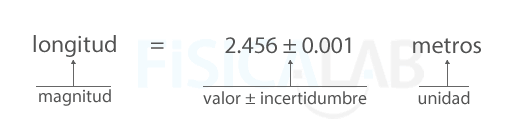
Dado que todas las medidas están afectadas por un error experimental, en el mundo científico es común hacer constar cada resultado obtenido en una medición junto con la incertidumbre sobre esa medida. La incertidumbre es un valor numérico que se obtiene por medio de dos nuevos conceptos denominados error absoluto y error relativo. 

Medición científica

Cada resultado de una medición viene dado por el valor númerico de la medición acompañado de un valor de incertidumbre sobre la medida.

A continuación vamos a estudiar como calcular estos dos tipos de error. ¿Estás preparado?.

Error absoluto

El error absoluto de una medida (${\epsilon }_a$) es la diferencia entre el valor real de la medida ($\overline{X}$) y el valor que se ha obtenido en la medición ($X_i$). 

$${\epsilon }_a=\overline{X}-X_i$$

El error absoluto puede ser un valor positivo o negativo, según si la medida es superior al valor real o inferior y además tiene las mismas unidades que las de la medida.

Cálculo del error absoluto

Para calcular el error absoluto de una medida es imprescindible conocer en primer lugar qué valor se considera como real. Por norma general ese valor es la media de los valores obtenidos al realizar un número n de mediciones en las mismas condiciones.

Con el fin de facilitar su cálculo cada uno de los valores obtenidos tras cada medición (X_i) se suelen escribir en una tabla junto con las veces que se produce a lo largo de todas las mediciones (f_i). Por ejemplo, imagina que pesamos 20 veces un mismo objeto (n = 20). Para representar los valores obtenidos se suele realizar una tabla como la siguiente:

Esta tabla muestra que al medir hemos obtenido el valor 3.45 g 2 veces, 3.40 g 3 veces, 3.52 g 5 veces, etc...

A continuación le añadimos una columna que muestra la multiplicación de la medida por la frecuencia de cada fila , incluyendo al final la suma de los valores de esta nueva columna:

La media de las medidas obtenidas ($\overline{X}$) será este valor X_i·f_i dividido por el número de medidas que hicimos ( n = 20 ):

$$\overline{X}=\sum _{i=1}^n\frac{X_i·f_i}{n}=\frac{\sum _{i=1}^{20} X_i·f_i}{20}=\frac{69.75}{20}=3.4875$$

Como hemos comentado anteriormente, esta media que hemos calculado es el valor que consideraremos como real. Dado que el error absoluto (${\epsilon }_a$) de cada medida es la diferencia entre el valor real  y el valor obtenido en la medición, vamos a añadir una nueva columna en la que se restan ambos valores:

De esta forma tenemos representados en la tabla todos los errores absolutos de cada uno de los valores de las medidas que hemos realizado.

Imprecisión absoluta

Una vez que hemos calculado el error absoluto de cada una de las medidas obtenidas, podemos calcular lo que se denomina imprecisión absoluta. La imprecisión absoluta se puede considerar como el error absoluto del conjunto de medidas que hemos realizado. Mas concretamente:

La imprecisión absoluta (Ea) es la media de los errores absolutos tomados con signos positivos:

$$Ea=\frac{{\displaystyle \sum _{i=1}^n}\left|\overline{X}-X_i\right|}{n}$$

En el ejemplo que nos ocupa:

$$Ea=\frac{{\displaystyle \sum _{i=1}^{20}\left|\overline{X}-X_i\right|}}{n}=\frac{0.1925}{20}=0.009625 g$$

¿Para qué sirve el error absoluto?

El error absoluto es un indicador de la imprecisión que tiene una determinada media. De hecho, cuando se proporciona el resultado de una medida suele venir acompañada de dicha imprecisión.

Ejemplo: Imagina que al medir un determinado objeto con un instrumento de precisión ± 1 cm obtenemos el valor de 23.5 cm. Si adicionalmente sabemos que la imprecisión absoluta de esa medida es 0.2 cm, entonces el resultado de esa medición se representa como: 23.5 cm ± 0.2 cm donde el valor real de la magnitud queda incluida en el intervalo 23.3 cm <= 23.5 cm <= 23.7 cm.

De forma general:

1. Si únicamente realizamos una sola medición con el instrumento de medida, el resultado final será el valor leído ± la precisión del instrumento de medida.

2. Si realizamos n medidas en las mismas condiciones, tomaremos como valor la media aritmética (X) ± el menor valor entre la imprecisión absoluta y la precisión del instrumento de medida.

Error relativo

Es el cociente entre el error absoluto y el valor que consideramos como exacto (la media). Al igual que el error absoluto puede ser positivo o negativo porque puede se puede producir por exceso o por defecto y al contrario que él no viene acompañado de unidades. 

$${\epsilon }_r=\frac{{\epsilon }_a}{\overline{X}}$$

De igual forma, se puede multiplicar por 100 obteniéndose así el tanto por ciento (%) de error.

$${\epsilon }_r=\frac{{\epsilon }_a}{\overline{X}}·100 \%$$

Como ejemplo podemos calcular el error relativo sobre nuestro ejemplo.  De esta forma obtenemos que:

$${\epsilon }_r=\frac{9.625·{10}^{-3}}{3.4875}·100 \%=0.27 \%$$

¿Para qué sirve el error relativo?

El error relativo tiene la misión de servir de indicador de la calidad de una medida. Para entender este concepto utilizaremos otro ejemplo. Imagina que se comete un error absoluto de 1 metro al medir una finca de 200 metros y otra de 3000. Si calculamos los errores relativos en ambas mediciones tenemos que son 1/200 y 1/3000. Dado que en la segunda medición el error relativo es más pequeño quiere decir que la calidad de la medida es mucho mejor que la de la primera. De hecho si lo piensas, bien es mucho mejor equivocarse en un metro cuando cuento 3000 metros que cuando cuento 200 metros.

Cuando se realizan una medición se considera que su calidad es mucho mayor cuanto más pequeño es el error relativo que se comete.