Velocidad Instantánea

El concepto cotidiano de velocidad surge cuando apreciamos la rapidez o lentitud con que se mueve un cuerpo. De alguna manera relacionamos el desplazamiento realizado con el tiempo invertido en él. En este apartado vamos a precisar qué es la velocidad física, también conocida como velocidad instantánea o, simplemente, velocidad. Para entenderlo bien, te recomendamos que previamente leas el apartado en el que te presentamos la velocidad media.

Velocidad instantánea

La velocidad física de un cuerpo en un punto o velocidad instantánea es la que tiene el cuerpo en un instante específico, en un punto determinado de su trayectoria.

La velocidad es una magnitud vectorial. Su ecuación de dimensiones viene dada por [v]= [L][T]^-1

¿Cómo se deduce la expresión de la velocidad instantánea?

Para definir el concepto de velocidad instantánea con precisión vamos a partir del concepto de velocidad media que hemos estudiado con anterioridad y vamos a ayudarnos de la gráfica de la figura.

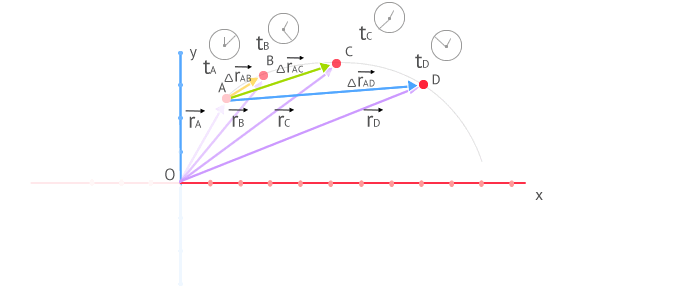
El procedimiento para definir la velocidad instantánea o, simplemente, velocidad en un punto A consiste en calcular la velocidad media entre A y un punto lo más próximo posible a A. Esto se traduce en calcular la velocidad media en un intervalo de tiempo lo más pequeño posible. En la gráfica puedes ver el vector de posición del punto A y del resto de puntos B, C y D. Estos son ${\overrightarrow{r}}_A$ , ${\overrightarrow{r}}_B$  , ${\overrightarrow{r}}_C$  y ${\overrightarrow{r}}_D$  respectivamente. Además está representado el vector desplazamiento entre A y cada uno de los puntos B, C y D. Estos son $∆{\overrightarrow{r}}_{AB}$ , $∆{\overrightarrow{r}}_{AC}$ y $∆{\overrightarrow{r}}_{AD}$ respectivamente. Como puedes ver en la gráfica anterior, a medida que el segundo punto es más próximo a A, el vector desplazamiento, se va haciendo tangente a la trayectoria y su módulo se aproxima al valor del espacio recorrido sobre la trayectoria.

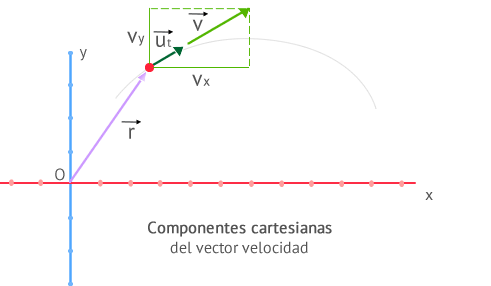
Lo más común es que encuentres el vector velocidad escrito mediante sus componentes cartesianas quedando:

• vector velocidad  en 3 dimensiones coordenadas cartesianas:

  $$\overrightarrow{v}=v_x\overrightarrow{i}+v_y\overrightarrow{j}+v_z\overrightarrow{j}=\left(\underset{∆t\to 0}{\lim }\frac{∆x}{∆t}\right)\overrightarrow{i}+\left(\underset{∆t\to 0}{\lim }\frac{∆y}{∆t}\right)\overrightarrow{j}+\left(\underset{∆t\to 0}{\lim }\frac{∆z}{∆t}\right)\overrightarrow{j}=\frac{dx}{dt}\overrightarrow{i}+\frac{dy}{dt}\overrightarrow{j}+\frac{dz}{dt}\overrightarrow{j}$$

• vector velocidad en 2 dimensiones coordenadas cartesianas:

  $$\overrightarrow{v}=v_x\overrightarrow{i}+v_y\overrightarrow{j}=\left(\underset{∆t\to 0}{\lim }\frac{∆x}{∆t}\right)\overrightarrow{i}+\left(\underset{∆t\to 0}{\lim }\frac{∆y}{∆t}\right)\overrightarrow{j}=\frac{dx}{dt}\overrightarrow{i}+\frac{dy}{dt}\overrightarrow{j}$$

También es posible que, al igual que cualquier otro vector, lo encuentres escrito en función de su módulo. Para ello basta multiplicar el módulo del vector velocidad por un vector unitario con la misma dirección y sentido que $\overrightarrow{v}$  y que llamaremos ${\overrightarrow{u}}_t$  por ser tangente a la trayectoria.

$$\overrightarrow{v}=v\cdot {\overrightarrow{u}}_t$$

Como puedes observar, la velocidad instantánea es una magnitud vectorial que cumple:

• Su módulo se puede expresar:

  • En función del módulo del vector desplazamiento o en función del espacio recorrido:

    $$\left|\overrightarrow{v}\right|=\underset{∆t\to 0}{\lim }\left|{\overrightarrow{v}}_m\right|=\underset{∆t\to 0}{\lim }\frac{\left|∆\overrightarrow{r}\right|}{∆ t}=\underset{∆t\to 0}{\lim }\frac{∆s}{∆ t}$$

  • Cuando el vector velocidad se expresa mediante coordenadas cartesianas en 3 dimensiones:

    $$\left|\overrightarrow{v}\right|=\sqrt{v_x^2+v_y^2+v_z^2}$$

  • Cuando el vector velocidad se expresa mediante coordenadas cartesianas en 2 dimensiones:

    $$\left|\overrightarrow{v}\right|=\sqrt{v_x^2+v_y^2}$$
• Su dirección es tangente a la trayectoria (la toca en un sólo punto).
• Su sentido es el mismo que el del movimiento

Conclusión

En este apartado hemos definido el concepto de velocidad instantánea a partir de la velocidad media, hemos estudiado su módulo, su dirección y su sentido. Aunque hemos tratado distintos puntos de vista y distintas expresiones para el vector velocidad y su módulo, normalmente calcularás la velocidad como la derivada del vector posición respecto al tiempo.