Capacidad Eléctrica
Capacidad Eléctrica
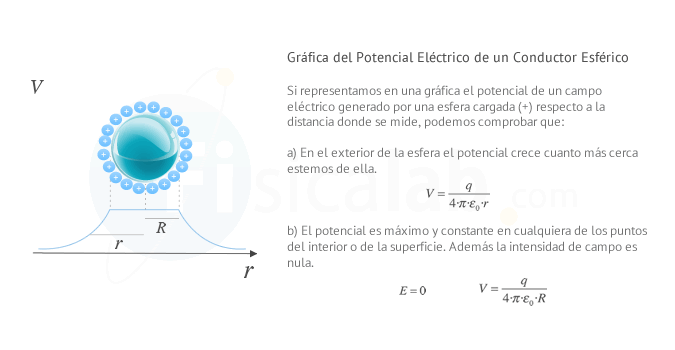
Si estudiamos detenidamente la expresión del potencial eléctrico creado por una carga puntual, puedes comprobar que a medida que la distancia se hace más pequeña (r→0) su valor V tiende al infinito (V→∞).
Sin embargo en la vida cotidiana no disponemos de cargas aisladas, sino que generalmente las cargas se encuentran asociadas en conductores no puntuales, y esta condición no se cumple para ellos.

En los conductores no puntuales la cargas se mueven libremente y se distribuyen de tal forma que la repulsión entre ellas se hace mínima, dejando que el exceso de carga se concentre únicamente en la superficie de los conductores, dejando libre de carga el interior.
Un conductor que se encuentra en equilibrio eléctrico tiene su exceso de carga repartido por su superficie. El potencial eléctrico en cualquier punto de su interior y de su superficie es el mismo y el campo eléctrico en su interior es nulo.
A partir de esta realidad, podemos definir una nueva magnitud escalar denominada capacidad eléctrica.
La capacidad eléctrica de un conductor es una magnitud escalar que relaciona la carga almacenada en un conductor y el potencial que adquiere de forma aislada.
donde:
- C es la capacidad eléctrica. En el S.I. se mide en faradios (F).
- q es el exceso de carga del conductor. En el S.I. se mide en culombios (C).
- V es el potencial eléctrico en cualquier punto del conductor. En el S.I. se mide en voltios (V).
La capacidad eléctrica siempre es una cantidad positiva y depende de la geometría del conductor.
Unidad de Capacidad Eléctrica
La unidad de capacidad eléctrica en el Sistema Internacional de Unidades (S.I.) es el faradio y se define como la capacidad que posee un conductor que al ser cargado con un culombio adquiere un potencial de un voltio.
El faradio, al igual que el culombio, se trata de una unidad muy grande por lo que es común que debamos trabajar con submúltiplos de esta. A continuación puedes encontrar algunos de los más utilizados:
- Milifaradio. 1 mF = 10-3 F
- Microfaradio. 1 µF = 10-6 F
- Nanofaradio. 1 nF = 10-9 F
- Picofaradio. 1 pF = 10-12 F
Superficies Equipotenciales
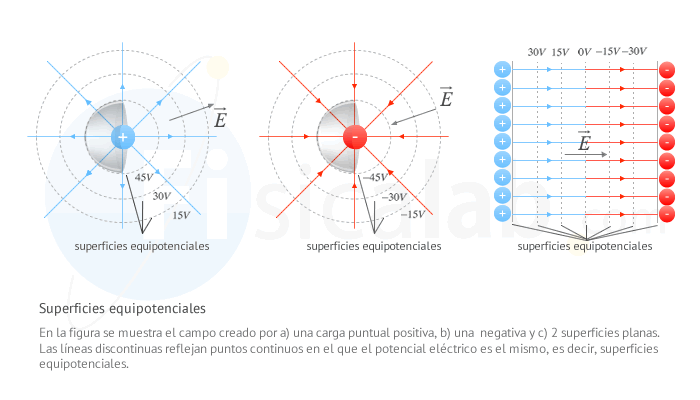
Los puntos contiguos de un campo eléctrico que tienen el mismo potencial eléctrico reciben el nombre de superficie equipotencial. Si aplicamos esta definición a los conductores, dado que todos ellos tienen el mismo potencial en su exterior, su superficie es una superficie equipotencial.
Dichas superficies se caracterizan principalmente porque son perpendiculares a las líneas de fuerza en cualquier punto del campo eléctrico.
Las superficies equipotenciales son esféricas si el campo eléctrico es originado por cargas puntuales y planas en el caso de que sean creadas por conductores planos.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
