Introducción al Concepto de Energía Potencial Eléctrica
Energía Potencial Eléctrica
Cuando hablamos de la energía potencial gravitatoria estudiamos que un cuerpo que se encuentra a determinada altura de la superficie de la Tierra adquiere una determinada cantidad de energía potencial provocada por la acción de la fuerza gravitatoria. De igual forma, un cuerpo cargado que sufre la acción de una fuerza eléctrica adquiere energía potencial electrostática.
La energía potencial eléctrica que posee una carga puntual q1 en presencia de otra carga puntual q2 que se encuentran separadas cierta distancia es
donde:
- Ep es la energía potencial eléctrica. En el S.I. se mide en Julios (J).
- q1 y q2 son los valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
- r es el valor de la distancia que las separa. En el S.I. se mide en metros (m).
- K es la constante de la ley de Coulomb. Para el vacío su valor es aproximadamente 9·109 N·m2/C2 utilizando unidades en el S.I.
Date cuenta que la energía potencial eléctrica es:
- positiva si las cargas poseen el mismo signo y negativa si tienen signos distintos.
- nula cuando la distancia de separación es infinita.
Relación entre el trabajo eléctrico y la energía potencial eléctrica
Como ocurre con todas las fuerzas conservativas, existe una relación entre el trabajo eléctrico y la energía potencial eléctrica. En concreto, el trabajo que realiza una fuerza eléctrica para desplazar una carga desde un punto A hasta otro B puede expresarse de la siguiente forma:
o lo que es lo mismo:
Fuerzas Externas contrarias a la Fuerza Eléctrica
Como ya hablamos en el apartado de trabajo eléctrico, este es el trabajo que realizan las fuerzas eléctricas y no debemos confundirlo con el trabajo que puede realizar una fuerza externa en contra de las fuerzas eléctricas para intentar aproximar dos cuerpos cargados con el mismo signo (que apriori intentarán separarse) o alejar dos cuerpos cargados con distinto signo (que apriori intentarán unirse). El trabajo que realiza dicha fuerza (Wf) se relaciona con el trabajo eléctrico (We) y la energía potencial eléctrica de la siguiente forma :
A continuación, vamos a estudiar que esta relación se cumple en los dos casos comentados anteriormente.
Cargas con distinto signo
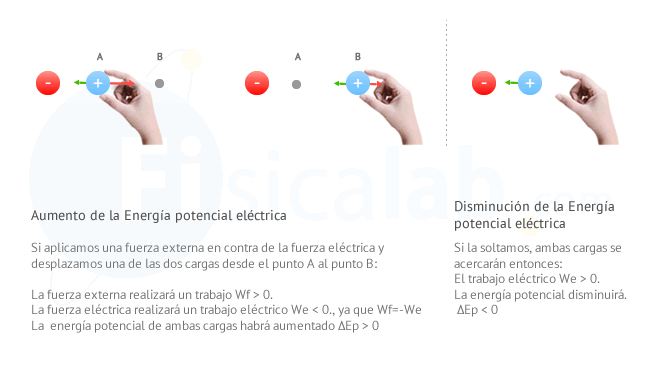
Imagina dos cargas fijas, una positiva y otra negativa. En principio, dado que se trata de cargas con distinto signo en cada una de ellas aparecerá una fuerza de atracción hacia la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más alejado. Al hacer esto:
- Si aplicas la definiciónde trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
- Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0).
- Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).
En resumidas cuentas, el trabajo que realiza la fuerza externa al alejarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de acercarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.
Cargas del mismo signo
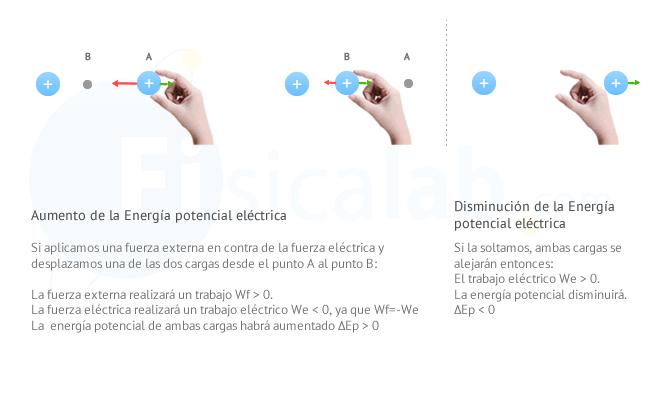
Ahora, imagina dos cargas fijas del mismo signo (positiva o negativa). En principio, dado que se trata de cargas con signos iguales en cada una de ellas aparecerá una fuerza de repulsión en contra de la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más cercano. Al hacer esto, como en el caso anterior:
- Si aplicas la definiciónde trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
- Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0).
- Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).
El trabajo que realiza la fuerza externa al acercarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de alejarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.
Fíjate que tal y como indicamos en la fórmula inicial, cuando se aplica la fuerza externa, el signo del trabajo del campo eléctrico es exactamente el contrario al del trabajo realizado por la fuerza eléctrica y al de la diferencia de energía potencial.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:
