Ecuación de una Parábola Vertical
Una parábola es el lugar geométrico de los puntos de un plano en los que la distancia a un recta llamada directriz es igual a la distancia a un punto fijo (que no pertenece a la directriz) llamado foco. ¿Esta definición te resulta complicada? No te preocupes, observa la siguiente imagen.
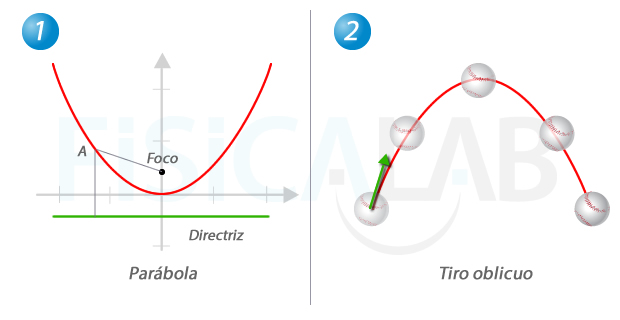
Parábola
A la izquierda, en rojo, puedes ver la forma de una parábola en el plano. Cualquier punto de la misma, como el punto A, dista igual distancia del foco que de la recta directriz. Tu día a día está lleno de situaciones en las que aparecen parábolas. Por ejemplo, a la derecha puedes ver la trayectoria de una pelota cuando la lanzas oblicuamente. Como ves, es una parábola con las ramas hacia abajo.
Aunque no son las únicas, en este apartado nos centraremos en las parábolas verticales, como las de la figura. Probablemente ya estés familiarizado con ellas, aunque no te hayas dado cuenta aún...
Expresión matemática
La ecuación de una parábola vertical corresponde a un polinomio de segundo grado:
Donde a, b y c son constantes.
| Ecuación | Valores a,b,c |
| y=3x2-x+2 | a=3 ; b= -1 ; c = 2 |
| y=x2+2x | a=1 ; b= 2 ; c = 0 |
| y=-x2+2 | a=-1 ; b= 0 ; c = 2 |
Representación gráfica
A partir de la expresión anterior, puedes ir dando valores a la x para ir obteniendo los valores de y correspondientes, y así obtener una seria de puntos (x,y) que puedas representar en el plano. Para ayudar a tu representación puedes tener en cuenta lo siguiente:
Ramas
- Si a>0 las ramas de la parábola están hacia arriba
- Si a<0 las ramas de la parábola están hacia abajo
Vértice
La coordenada x del vértice, xv, se calcula según:
La coordenada y del vértice, yv, se calcula sustituyendo la xv en la expresión de la parábola:
- El vértice de la parábola es el menor valor de y si las ramas están hacia arriba (a>0)
- El vértice de la parábola es el mayor valor de y si las ramas están hacia abajo (a<0)
Corte con el eje y
Una parábola tiene un punto de corte con el eje y. Este punto (xcy,ycy) siempre cumple que su coordenada x es cero, es decir, xcy=0. Por tanto, para encontrarlo hacemos la x 0 y vemos el valor de y en la expresión:
Efectivamente, el punto de corte con el eje y siempre es (0,c).
Corte con el eje x
Una parábola puede cortar al eje x en dos puntos, en un punto o en ningún punto. Los puntos de corte de la parábola con el eje x, (xcx,ycx), siempre cumplen que sus coordenadas y valen cero, es decir, (xcy,0). Para calcular la coordenada xcx sustituimos la y por cero en la expresión de la parábola y resolvemos la ecuación de segunda grado que nos queda.
- Si la ecuación tiene dos soluciones xcx1 y xcx2, existen dos puntos de corte: (xcx1,0) y (xcx2,0)
- Si la ecuación tiene una sola solución xcx1, existe un único punto de corte (coincidirá con el vértice): (xcx1,0)
- Si la ecuación no tiene solución entonces la parábola no corta al eje x en ningún punto
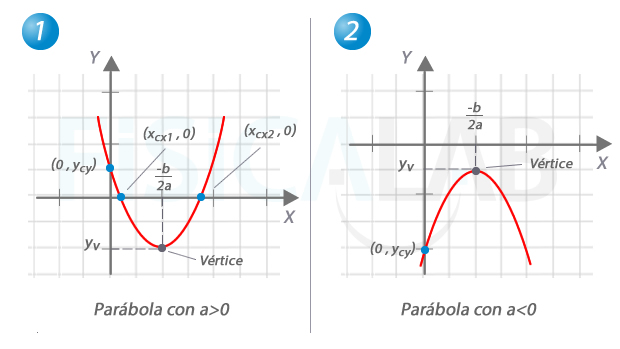
Representación gráfica de parábolas
En 1, parábola con las ramas hacia arriba. En ella el vértice es el punto mínimo. A la derecha otra parábola con las ramas hacia abajo. Observa que esta última no presenta punto de corte alguno con el eje x
Parábola simétrica respecto al eje y
Cuando en la expresión general b=0 la parábola es simétrica respecto al eje y. En estos casos la parábola puede expresarse tal y como aparece en la siguiente tabla. En ella podemos distinguir dos constantes importates:
- La constante a, que determina la amplitud de la parábola.
- Y la constante y0 que es la ordenada en el origen, es decir, donde la parábola corta al eje y.
| Fórmula | Representación |
|
|
Para representar cualquier tipo de parábola puedes utilizar nuestro simulador de polinomios. Ten presente que los coeficientes constantes a, b y c corresponden en la simulación con a=a2, b=a1 y c=a0.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.

