Velocidad de la Luz

Aunque hoy sabemos que la velocidad de la luz es finita, hasta la época de Galileo era común la creencia de que la luz se transmistía instantáneamente. Galileo trató en vano de determinarla, pero consiguió allanar el camino para la elaboración de métodos que lo consiguiesen. A día de hoy:

A continuación estudiaremos:

• Qué es y cómo usar el índice de refracción para calcular la velocidad de la luz en un medio distinto del vacío
• Dos experimentos clásicos para determinar la velocidad de la luz, el de Roemer y el de Fizeau, así como las variaciones que introdujo Foucault

¿Empezamos?

Índice de refracción

El valor de la velocidad de la luz es constante en un mismo medio, sin embargo, cuando se produce un cambio a otro medio transparente, el valor de la velocidad también cambia, tal y como se pone de manifiesto en el fenómeno de la refracción. En el caso de la luz es habitual usar el índice de refracción absoluto y el relativo para cuantificar este cambio.

El índice de refracción absoluto de un medio nos sirve para calcular la velocidad de la luz en él y cuenta con las siguientes características:

• Su valor en el vacío es n=1 para cualquier longitud de onda
• En cualquier otro medio, su valor depende de la longitud de onda y es una propiedad característica de cada medio para dicha longitud de onda n(λ). Esto implica que la velocidad de la luz en un medio distinto del vacío depende de la longitud de onda
• Su valor es siempre mayor o igual que uno, pues c>v. A mayor n, menor es la velocidad de la luz en ese medio
• Cuando un medio tiene un índice de refracción mayor que otro se dice que es más refrigente
• Se puede relacionar con la permitividad relativa ε_r y la permeabilidad relativa μ_r del medio según $n=\sqrt{{\epsilon }_r·{\mu }_r}$  Y dado que, a las frecuencias de la luz, normalmente μ_r = 1, nos queda $n=\sqrt{{\epsilon }_r}$ 

El índice de refracción relativo pone de manifiesto que cuando la luz pasa de un medio a otro más refrigente, se propaga a menor velocidad y menor longitud de onda.

Comprobación

$$\begin{gathered} n_{2,1}=\frac{n_2}{n_1}\stackrel{\left[1\right]}{=}\frac{{\displaystyle c/v_2}}{{\displaystyle c/v_1}}=\frac{v_1}{v_2}\stackrel{\left[2\right]}{=}\frac{f·{\lambda }_1}{f·{\lambda }_2}=\frac{{\lambda }_1}{{\lambda }_2} \\ \left[1\right]n=c/v \\ \left[2\right]v=f·\lambda \end{gathered}$$

Método de Roemer

El astrónomo Olaf Roemer (1644 - 1710) de origen danés fue el primero en medir con éxito, de manera aproximada, la velocidad de la luz. Para ello estudió las órbitas del satélite Ío de Júpiter al pasar detras del planeta. La siguiente figura nos ayudará a comprender, de manera simplificada, su método:

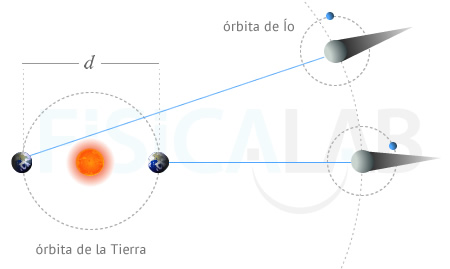
Método Roemer

El cono de sombra que crea el Sol tras Júpiter es atravesado periódicamente por Ío. Esto hace que, desde la Tierra, Ío desaparezca y reaparezca cada cierto tiempo, oculto en dicha sombra. Las posiciones en las que se ha dibujado la Tierra corresponden a la más cercana y a la más alejada de Júpiter respectivamente, y ayudaron a Roemer a medir la velocidad de la luz por primera vez.

Roemer observó que, cuando Júpiter se hallaba a la distancia mínima de la Tierra, el tiempo entre dos salidas sucesivas de la sombra era de 42 h y 28 minutos, aproximadamente. Por contra, cuando la Tierra estaba en su punto más alejado el periodo se incrementaba 22 minutos.

La conclusión era que el incremento de tiempo se debía al lapso de tiempo que tardaba la luz en recorrer la distancia adicional. Dicha distancia, representada en la figura por d , correspondía al diámetro de la Tierra alrededor del Sol, que en aquella época no se conocía con total precisión. Esto, unido a las imperfecciones de sus aparatos de medida, le llevo a calcular que la velocidad de la luz era de v=2.14·10⁸ ( a partir de una simple relación v = d/t siendo t = 22·60 segundos ) . Aunque imprecisa, bastó para desterrar la idea de que la velocidad de la luz era infinita.

Método de Fizeau

El físico francés Armand H. L. Fizeau ( 1819 - 1869 )  diseñó, en 1849, un ingenioso experimento para medir la velocidad de la luz que le llevó a convertirse en la primera persona capaz de realizar una medida directa, en laboratorio, de tal magnitud. Para ello utilizó una rueda dentada, varias lentes y espejos y un foco de luz, dispuestos de manera similar a la siguiente figura:

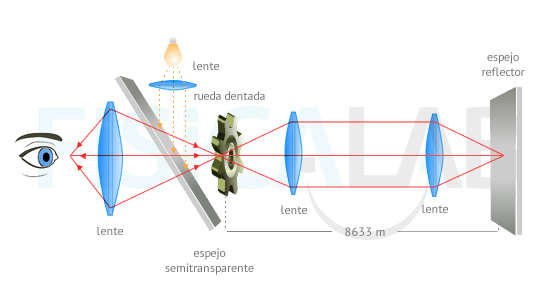
Método Fizeau

El pulso de luz emitido por la bombilla superior se refleja en el espejo semitransparente hacia la derecha. Si el pulso es capaz de pasar entre los dientes de la rueda, que puede estar en rotación, se reflejará en un espejo situado a más de 8 km de distancia y volverá hacia la rueda. En caso de que esta, de nuevo, deje el pulso pasar entre sus dientes, el observador de la izquierda percibirá el pulso original, tras haber pasado por el espejo semitransparente.

Es evidente que cuando la rueda está parada la luz será visible siempre que pase por un hueco. También es evidente que si la rueda se encuentra en una posición tal que bloquea el paso de luz con un diente, el pulso no será percibido por el observador.  Cuando comenzamos a girar la rueda aumentando poco a poco su velocidad, la luz será percibida de forma intermitente, en función de si pasa por un hueco o la bloquea un diente. Sin embargo, Fizeau observó que, si conseguía aumentar la velocidad de rotación de la rueda lo suficiente, el pulso no era visible en absoluto. Esto ocurría cuando el pulso quedaba siempre bloqueado por un diente. En un intervalo de la rotación un determinado diente bloquea la ida, cuando llega el hueco correspondiente el rayo pasa, pero para cuando el rayo ha regresado de nuevo a la rueda, el siguiente diente bloquea la vuelta.

De esta manera, conocida la velocidad de rotación de la rueda y el número de dientes, es posible determinar la velocidad de la luz. La primera medida que realizó Fizeau arrojó un valor de 315000 km/s. 

Mejora de Foucault

Jean Bernard Léon Foucault ( 1819 - 1868 ) fue un físico francés que había sido, durante mucho tiempo, amigo y colaborador de Fizeau. Entre otras cosas fue reconocido por demostrar la rotación de la Tierra a través del péndulo de Foucault, pero su nombre aparece en este apartado debido a sus importantes contribuciones a la determinación de la velocidad de la luz.

Parece ser que, tras haber trabajado un tiempo con Fizeau, hubo una disputa entre ambos que llevó a Foucault a desarrollar, en 1850, un experimento para medir la velocidad de la luz por su propia cuenta. Concretamente, sustituyó la rueda dentada por un espejo rotativo, tal y como se indica en la figura inferior:

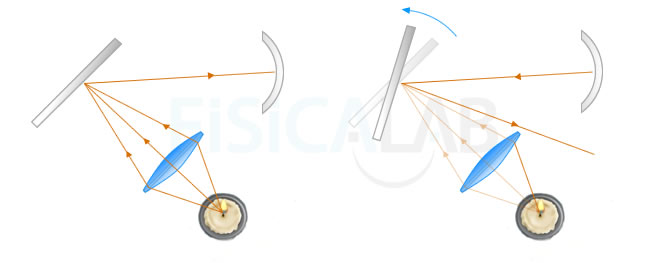
Esquema del experimento con espejo rotativo ideado por Foucault

El principio básico es que un pulso es reflejado en un espejo capaz de rotar. La luz reflejada se enfoca, a través de una lente en un espejo fijo que devuelve la luz al espejo anterior. En función del ángulo que guarda el rayo de luz devuelto con el rayo original, se puede deducir la velocidad de la luz en el medio. Observa que este ángulo cambia en función del medio en el que se propague la luz.

Si el espejo rotativo está en reposo, la luz vuelve por el mismo camino que utilizó en la ida (θ = 0). Si está en rotación, con la suficiente velocidad, en el reflejo que sigue el rayo a la vuelta del espejo fijo se producirá un cierto desvío, determinado por θ y causado por el ángulo que haya girado el espejo rotativo desde que produjo la primera reflexión, de ida del rayo, hasta que produce la segunda, de vuelta del rayo.

Con este método Foucault pudo medir la velocidad de la luz, no sólo en el aire, sino también en el agua, demostrando que era menor en esta y asestando un golpe definitivo a la teoría corpuscular de la luz de Newton. El espejo usado por primera vez por Foucault era reflectante sólo por una de sus caras, lo que daba a la luz reflejada un aspecto 'parpadeante'. Además existían otros pequeños problemas que fueron poco a poco siendo mejorados en sucesivos experimentos, no sólo por Foucault si no también por físicos como el americano Albert A. Michelson ( 1852 - 1931 ) quién consiguió el valor de 2.9974·10⁸ m/s para la velocidad de la luz en el vacío, muy próximo al valor que hoy consideramos válido.