Experimento de Fizeau

Datos

• Dientes de la rueda: 720
• Velocidad de giro: 12.66 r.p.s. = 12..66·2·π = 79.53 rad/s
• Distancia de separación rueda - espejo reflector: d = 8633 m

Consideraciones previas

En primer lugar debemos hacernos una representación mental del experimento. En la figura tienes una simplificación de la situación:

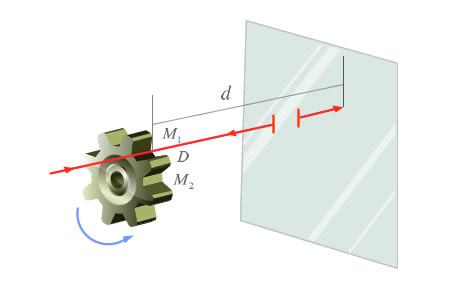
Como hemos visto en la descripción del experimento en teoría, a medida que la velocidad de la rueda aumentaba el rayo dejaba de hacerse visible. Concretamente nos señala el ejercicio que a la velocidad señalada, 79.53 rad/s ,se ocultaba completamente el rayo, lo cual quiere decir que todo rayo que consiguiera pasar por la muesca M₁ quedaba obstruido en su retorno tras la reflexión por el diente D. Hemos reducido de 720 a 8 el número de muescas para poder visualizar mejor la situación.

Resolución

Sabemos que la velocidad de la luz es constante y se mueve según un m.r.u. Por tanto podemos escribir:

$$v_{luz }=\frac{∆s}{∆t}$$ 

El espacio de referencia en el experimento es, justamente 2·d, es decir 2·8633 m = 17266 m. Ese es el espacio recorrido por la luz mientras la rueda gira lo suficiente como para que, al llegar de nuevo la luz a la rueda, se encuentre con un diente (el comienzo del diente D). Teniendo presente que la rueda tiene 720 dientes, tendrá el mismo número de muescas. Puedes comprobar esta última afirmación dibujando una rudimentaria rueda dentada de 4 dientes. Verás como también tiene, necesariamente, 4 muescas.

Por consiguiente, si la rueda pasa a través de M₁ y queda bloqueada en la rueda adyacente D, la rueda ha girado 1/(720·2) de vuelta en el tiempo que la luz ha ido al espejo, se ha reflejado y ha vuelto a la rueda. Así, de esta sencilla relación podemos obtener el tiempo buscado en la expresión anterior:

$$\omega =\frac{∆\phi }{∆t}\Rightarrow ∆t=\frac{∆\phi }{\omega }$$

En relación a ∆φ, su valor es justamente [∆φ/(720·2)]·2·π = 0.043 rad, con lo que podemos sustituir datos quedando:

$$∆t=\frac{∆\phi }{\omega }=\frac{0.043}{79.53}=5.4·{10}^{-5} s$$

$$v_{luz }=\frac{∆s}{∆t}=\frac{17266}{5.4·{10}^{-5}}=3.19·{10}^8 m/s$$

Para que el rayo de luz vuelve a verse completamente, el tiempo que tarda la luz en ir y volver debe ser suficiente para que el rayo vuelva a situarse en la posición que tenía en la muesca M₁, pero en M₂. Es decir, la rueda debe girar la muesca completa en la que estaba más el diente adyacente. Matemáticamente:

$$∆\phi =2·\frac{1}{720·2}=\frac{1}{720}vueltas =\hspace{0.17em}\frac{\pi }{360}rad$$

Por otro lado:

$$v_{luz }=\frac{∆s}{∆t}\Rightarrow ∆t=\frac{∆s}{v_{luz }}=\frac{2·8633}{3.19·{10}^8}=5.4·{10}^{-5}s$$

Y finalmente:

$$\omega =\frac{∆\phi }{∆t}=\frac{{\displaystyle \frac{\pi }{360}}}{5.4·{10}^{-5}}=161.23 rad/s =\hspace{0.17em}25.66 r.p.s$$