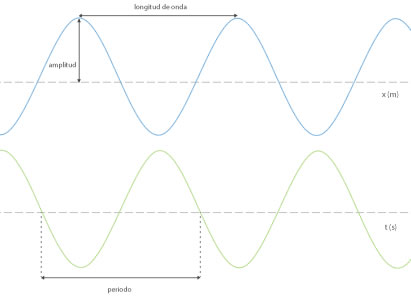
Ondas Armónicas

Podemos definir una onda como una perturbación que se propaga de un punto a otro de un medio sin que exista transporte neto de materia, pero sí transmisión de energía. Cuando una onda se propaga produce variaciones en algunas propiedades del medio que pueden ser expresadas matemáticamente (por ejemplo la posición de las partículas que vibran en torno a un punto de equilibrio en una onda que se propaga en una cuerda, o la presión del aire en el caso del sonido). Si podemos expresar estas variaciones espaciales y temporales del medio mediante funciones senos o cosenos decimos que la onda es armónica. En este apartado estudiaremos las ondas armónicas unidimensionales, es decir, aquellas que se propagan en una sola dirección (que solemos llamar x). Vamos a tratar:

• El concepto de onda armónica
• Los parámetros que la caracterizan
• Su ecuación o ecuaciones características
• Las distintas velocidades que se pueden definir en una onda

Estudiando de manera rigurosa las ondas armónicas unidimensionales simplificaremos enormemente el tratamiento matemático que suele estar asociado a las ondas, pero no perderemos rigor físico y nos servirán de base para análisis más complejos que pueden hacerse en niveles más avanzados. ¿Empezamos?

Concepto

Si atas una cuerda a un gancho de la pared, tomas el otro extremo con tu mano y la agitas periodicamente en sentido vertical, estarás generando un tren de ondas transversales. Observa el perfil de la cuerda, al cabo de cierto tiempo. ¿Te recuerda a algo? Quizás la siguiente imagen te ayude a aclararte.

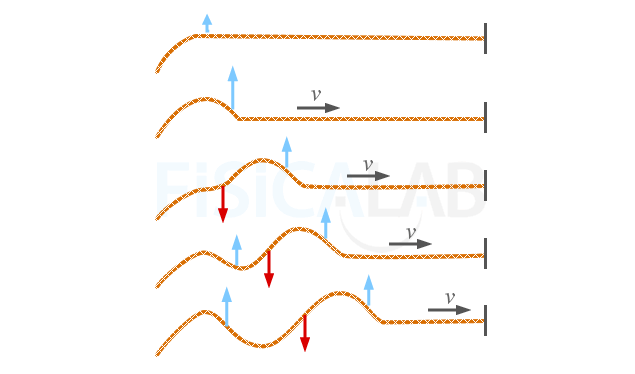
Onda en una cuerda

Agitando el extremo de una cuerda atada a la pared obtenemos una onda armónica. Su perfil instantáneo, al cabo de cierto tiempo, se asemeja a una función seno o coseno (una sinusoide).

Las ecuaciones anteriores y sus parámetros son descritos en detalle en los siguientes subapartados. De momento queremos llamar tu atención sobre la similitud que guardan con las ecuaciones del m.a.s. Efectivamente, las ondas armónicas son producidas por un oscilador armónico y cada punto del medio de propagación (cada punto de la cuerda de nuestro ejemplo) ejecuta un m.a.s.

Aunque no es frecuente encontrar ondas perfectamente armónicas en la naturaleza, sí que muchas ondas pueden considerarse una composición de estas. Este hecho fue descubierto por Jean-Baptiste Joseph Fourier y es comúnmente aplicado en diversos campos como, por ejemplo, las telecomunicaciones.

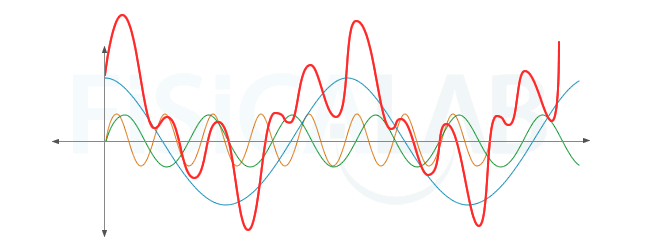
Composición de una onda a partir de otras armónicas 

En numerosas ocasiones podemos estudiar ondas complejas, como la roja, a partir de ondas armónicas más sencillas (azul verde y naranja).

Magnitudes características

Las ondas armónicas presentan una serie de parámetros que nos permiten caracterizarlas y que pasamos a definir:

• Elongación: Es la separación instantánea de cada punto del medio respecto a su posición de equilibrio. Su unidad de medida en el Sistema Internacional (S.I.) es el metro (m)

• Amplitud (A): Es el valor de elongación máxima. Su unidad de medida en el S.I. es el metro (m). Los valores de elongación de la onda armónica oscilan entre -A y A. A los puntos con máxima elongación (+A) se les suele llamar crestas. A los puntos en los que la elongación es mínima (-A) se les suele llamar valles

• Fase (φ): Se entiende por fase el estado de vibración de un punto de la onda. Decimos que dos puntos de la onda están en fase o que tienen igual fase cuando su elongación y la velocidad de su movimiento (velocidad de vibración) coinciden. Por el contrario, decimos que dos puntos se encuentran en oposición de fase o que tienen fase opuesta cuando las respectivas elongaciones y velocidades de vibración son justo las contrarias (igual valor, distinto signo). Una vez hayamos presentado la ecuación de una onda armónica estaremos en condiciones de introducir qué es la fase matematicamente.

• Longitud de onda (λ): Es la distancia entre dos puntos consecutivos que se encuentran en fase. Su unidad de medida en el S.I. es el metro (m). Refleja la periodicidad espacial de la onda armónica, ya que esta "se repite" (tiene igual forma) cada λ metros, como se evidencia en las gráficas en las que representamos la magnitud perturbada frente a la posición (gráficas y-x)

• Periodo (T): Es el tiempo que tarda la onda en recorrer una distancia igual a la longitud de onda. También se puede definir como el tiempo que tarda un punto cualquiera en realizar una oscilación completa en torno a su posición de equilibrio. Su unidad de medida en el S.I. es el segundo (s). Refleja la periodicidad temporal de la onda armónica, ya que esta se repite (tiene igual forma) cada T segundos,como se evidencia en las gráficas en las que representamos la magnitud perturbada frente al tiempo (gráficas y-t)

• Frecuencia (f): Es el número de oscilaciones por unidad de tiempo que un punto determinado del medio realiza en torno a su estado de equilibrio. Se define como la inversa del periodo y coincide con el número de longitudes de onda que pasan por un punto determinado del medio en una unidad de tiempo. Su unidad de medida en el S.I. es el hertzio (Hz), unidad que es la inversa del segundo (1 Hz = 1 s^-1). Se trata de un parámetro característico del foco por lo que la frecuencia mantiene su valor cuando la onda cambia de medio

  $$\boxed{f=1/T}$$

• Pulsación o frecuencia angular (ω): Permite expresar la frecuencia de las ondas de forma alternativa. Su unidad de medida en el S.I. es el radián por segundo (rad/s) y se define como:

  $$\boxed{\omega =2·\pi ·f=\frac{2·\pi }{T}}$$

• Velocidad de propagación (v): También se le conoce como velocidad de fase y es el desplazamiento efectuado por la onda por unidad de tiempo. Se puede entender como la rapidez a la que se propaga la onda. En general depende de las características del medio,como hemos visto en el caso de la velocidad de propagación de las ondas mecánicas, y no de las del foco por lo que es constante mientras el medio no modifique sus propiedades. No debe confundirse con la velocidad de vibración de las partículas individuales, como aclararemos más abajo. Su unidad de medida en el S.I. es el metro por segundo (m/s) y podemos calcularla, atendiendo a las características de la onda propagada, teniendo en cuenta que esta tarda un periodo (T segundos) en recorrer una longitud de onda (λ m), es decir:

  $$\boxed{v=\frac{\lambda }{T}=\lambda ·f}$$

• Número de onda (k): Se define como el número de longitudes de onda u ondas completas contenidas en una longitud de 2·π metros. Su unidad de medida en el S.I. es el metro a la menos uno (m^-1) ó, equivalentemente, el radián por metro (rad/m) y su expresión viene dada por:

  $$\boxed{k=\frac{2·\pi }{\lambda }=\frac{\omega }{v}}$$

  El parámetro número de onda también aparece en espectroscopia donde a veces se le llama frecuencia reducida y suele definirse de manera ligeramente distinta. Se trata del número de longitudes de onda u ondas completas contenidas en una unidad de longitud: k=1/λ

Experimenta y Aprende

Cargando...

Gráficas y magnitudes de onda armónica

La representación gráfica espacial y temporal de una onda nos ayuda a comprender sus magnitudes características. Pulsa sobre el botón play para comenzar a experimentar.

Ecuación

Se define la ecuación de una onda como la expresión que nos permite conocer el estado de vibración de cualquier punto del medio en cualquier instante. Para deducirla vamos a suponer una onda transversal generada por un oscilador armónico que se propaga a velocidad constante de izquierda a derecha a lo largo de una cuerda. Supondremos que no existe pérdida de energía en la propagación por lo que todos los puntos vibran con igual amplitud y frecuencia.

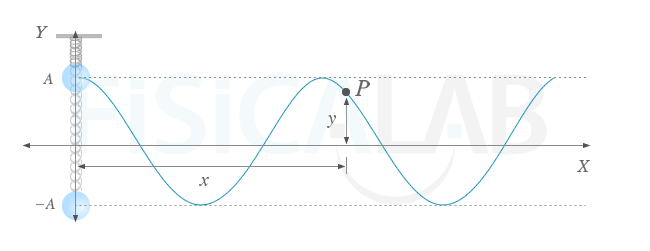
Onda generada en una cuerda por un oscilador armónico

El oscilador armónico de la figura atado a la cuerda azul genera una perturbación en ella que es, idealmente, una onda armónica de amplitud A. Dentro de la cuerda, cualquier punto P vibrará siguiendo el m.a.s del foco pero con un cierto retardo que depende de la distancia x a la que se encuentre del mismo.

La ecuación que rige el centro emisor, situado en el origen de coordenadas, es la ecuación del m.a.s:

$$y=A·\sin \left(\omega ·t+{\phi }_{\mathrm{f}}\right)$$

Donde ω es la frecuencia angular del foco, A su amplitud y φ_f es su fase inicial que determina el estado inicial de vibración, esto es, la posición y del foco en el instante t=0.

Observa que cualquier punto genérico P que diste una distancia x del foco vibrará de manera análoga a este, siguiendo un m.a.s., pero lo hará con un cierto retraso t', por lo que la ecuación con la que podemos describir la vibración del punto P será:

$$y=A·\sin \left(\omega ·\left(t-t\text{'}\right)+{\phi }_{\mathrm{f}}\right)$$

Por otro lado, sabemos que la onda tiene una velocidad de propagación constante por lo que el tiempo t' que tardará en llegar desde el origen a x vendrá dado por t'=x/v, quedando:

$$y=A·\sin \left(\omega ·\left(t-\frac{x}{v}\right)+{\phi }_f\right)\underset{\left[1\right]}{=}A·\sin \left(k·v·t-k·x+{\phi }_f\right)\underset{\left[2\right]}{=}A·\sin \left(k·x-k·v·t\underset{{\mathrm{\phi }}_0}{\underbrace{-{\mathrm{\phi }}_{\mathrm{f}}\pm \mathrm{\pi }}}\right)=A·\sin \left(k·\left(x-v·t\right)+{\phi }_0\right)$$

Donde hemos considerado:

$$\begin{gathered} \left[1\right]k=\frac{2·\mathrm{\pi }}{\lambda }=\frac{2·\mathrm{\pi }}{v·T}=\frac{\omega }{v} \\ \left[2\right]\sin \left(a-b\right)=\sin \left(b-a\pm \mathrm{\pi }\right) \end{gathered}$$

Si en lugar de considerar una onda viajera hacia la derecha la hubiésemos considerado hacia la izquierda, el desarrollo hubiese sido análogo salvo que el factor x-v·t sería x+v·t.

La expresión anterior es, precisamente, la que define a las ondas armónicas (aquellas cuya perturbación es producida por un oscilador armónico), tal y como habíamos considerado al principio del apartado, donde habíamos omitido la fase φ₀ por simplicidad ( φ₀=0 ). Observa que la expresión cumple con la ecuación de propagación de las ondas mecánicas $y=f\left(x\pm v·t\right)$ . Observa también la doble periodicidad de la onda respecto al espacio y al tiempo.

Finalmente, recuerda que, aunque hemos hecho nuestro desarrollo partiendo de una onda transversal propagándose en una cuerda para llegar a una ecuación general de ondas armónicas, su estudio es aplicable a ondas producidas en otros medios en los que se perturban otras magnitudes distintas de la posición y de las partículas. Este es el caso, por ejemplo, del sonido en el aire, en el que, podemos estudiar las diferencias de presión del aire como una composición de ondas armónicas. Es por esta razón que en ocasiones, en lugar de usar la variable y que suele hacer referencia a la posición, se utiliza la variable genérica ψ, quedando la ecuación general en la forma:

$$\psi \left(x,t\right)={\psi }_0·\sin \left(k·\left(x\pm v·t\right)+{\phi }_0\right)$$

Ondas armónicas y el sonido

Las ondas armónicas se pueden aplicar al estudio del sonido, ya que las variaciones de presión que se producen en el aire se pueden corresponder con funciones sinuosidades.

Fase de la onda

Ahora que hemos definido la ecuación de una onda armónica estamos en condiciones de estudiar matemáticamente el concepto de fase presentado anteriormente y que pueda dar lugar a ciertas confusiones:

• Llamamos fase o ángulo de fase y lo denotamos por φ al argumento de la función seno, es decir,

  $$\phi =k·\left(x\pm v·t\right)+{\phi }_0=2·\mathrm{\pi }·\left(\frac{x}{\lambda }\pm \frac{t}{T}\right)+{\phi }_0$$

  según la forma de la ecuación de onda señalada. Su unidad de medida en el Sistema Internacional (S.I.) es el radián

• Llamamos fase inicial a φ₀, ya que es el valor de la fase cuando x=0 y t=0

• Al valor que toma la diferencia de fase entre dos puntos ∆φ=φ₂-φ₁ se la denomina desfase. Su valor en cualquier instante depende de la distancia entre los puntos d=x₂-x₁ según:

  $$\begin{gathered} ∆\phi =\left[2·\mathrm{\pi }·\left(\frac{x_2}{\lambda }-\frac{t}{T}\right)-2·\mathrm{\pi }·\left(\frac{x_1}{\lambda }-\frac{t}{T}\right)\right]=\frac{2·\mathrm{\pi }}{\lambda }·\left(x_2-x_1\right)\Rightarrow \\ \Rightarrow \boxed{∆\mathrm{\phi }=2·\mathrm{\pi }·\frac{\mathrm{d}}{\mathrm{\lambda }}} \end{gathered}$$

• Como dijimos anteriormente, decimos que dos puntos x₁ y x₂ tienen igual fase o están en fase cuando tienen igual estado de vibración. Esto se traduce matemáticamente en que sus respectivas φ son equivalentes (φ₂=φ₁+2·π·n⇒∆φ=2·π·n con n ∈ Z) para cualquier instante t

  $$\begin{gathered} ∆\phi =\cancel{2·\mathrm{\pi }}·n=\cancel{2·\mathrm{\pi }}·\frac{x_2-x_1}{\lambda }\Rightarrow \\ \Rightarrow \boxed{x_2-x_1=n·\lambda } \end{gathered}$$

  Es decir, dos puntos están en fase si la diferencia entre sus distancias al foco es un múltiplo entero de la longitud de onda

• Como dijimos también anteriormente, dos puntos x₁ y x₂ tienen fase opuesta están en oposición de fase cuando su estado de vibración es justo el contrario. Esto se traduce matemáticamente en que sus respectivas φ están desfasadas π radianes (o cualquier múltiplo impar de π), para que el signo del seno sea el contrario (φ₂=φ₁+π·(2·n+1)⇒∆φ=π·(2·n+1) con n ∈ Z) para cualquier instante t

  $$\begin{gathered} ∆\phi =\cancel{\mathrm{\pi }}·\left(2·n+1\right)=2·\cancel{\mathrm{\pi }}·\frac{x_2-x_1}{\lambda }\Rightarrow \\ \Rightarrow \boxed{x_2-x_1=\left(2·n+1\right)·\frac{\lambda }{2}} \end{gathered}$$

  Es decir, dos puntos están en oposición de fase si la diferencia entre sus distancias al foco es un múltiplo entero impar de la semilongitud de onda

• En ocasiones el desfase se puede expresar, además de en radianes como es inmediato, en función de las longitudes de onda λ. Así, por ejemplo, dos crestas opuestas de una onda (A y -A) siempre se encuentran separadas d=λ/2 por lo que podemos decir que tienen un desfase de media onda (equivalente a π radianes o 180º)

Formas equivalentes

Existen muchas formas alternativas de escribir la ecuación general de una onda armónica. A partir de las definiciones de las magnitudes realizadas en este apartado podemos encontrar las siguientes equivalencias:

Puedes usar el scroll lateral si no puedes visualizar la tabla anterior completa en tu pantalla.

Observa que para definir una misma onda de dos formas equivalentes todos sus parámetros deberán permanecen iguales pero el valor de φ₀ será distinto según la expresión usada. Esto quiere decir que, por ejemplo:

$$y=3·\sin \left(\mathrm{\pi }·x-10·\mathrm{\pi }·t+\underset{{\phi }_0}{\underbrace{\frac{3·\mathrm{\pi }}{2}}}\right)=3·\cos \left(\mathrm{\pi }·x-10·\mathrm{\pi }·t-\underset{{\phi }_0\text{'}}{\underbrace{\mathrm{\pi }}}\right)$$

Si deseas comprobar tu mismo las equivalencias anteriores no olvides las siguientes relaciones trigonométricas:

$$\begin{gathered} \sin \left(a\right)=\cos \left(a-\mathrm{\pi }/2\right); \\ \sin \left(a-b\right)=\sin \left(b-a\pm \mathrm{\pi }\right); \\ \cos \left(a-b\right)=\cos \left(b-a\right); \end{gathered}$$

Tipos de velocidades en la onda armónica

En una onda existen dos velocidades muy distintas que, en ocasiones, suelen dar lugar a confusión. Ambas se miden en el Sistema Internacional en metros por segundo (m/s) pero sus semejanzas acaban ahí:

• Por un lado está la velocidad de fase o de propagación de la onda, de la que ya hemos hablado más arriba. Es la velocidad a la que la onda se propaga por el medio. Por ejemplo, cuando el oscilador armónico de nuestro ejemplo comienza a moverse, existe un retardo hasta que todos los puntos próximos comienzan a moverse. La velocidad de propagación depende del medio, como hemos visto en el caso de la velocidad de propagación de las ondas mecánicas, y es constante. Su valor puede ser calculado a partir de las características de la onda propagada según:

  $$v=\frac{\lambda }{T}=\lambda ·f$$

• Por otro lado está la velocidad de vibración de cada punto de la onda. Su valor es variable con el tiempo, siendo 0 en los puntos en los que la onda tiene amplitud A ó -A y máxima cuando la partícula pasa por su punto de equilibrio. Depende de la velocidad a la que vibra el foco emisor y su valor se obtiene derivando la ecuación de la onda respecto al tiempo, es decir:

  $$v=\frac{\partial y}{\partial t}$$