Flujo Eléctrico

¿Qué es el flujo de campo eléctrico?

El matemático y físico alemán Karl Friederich Gauss (1777-1855) estableció una relación entre el número de líneas de campo eléctrico que atraviesan una superficie cerrada y la carga almacenada en su interior.

Esta definición comprende dos conceptos importantes:

• Por un lado, el número de líneas de fuerza, que como ya estudiamos anteriormente es siempre proporcional al módulo de la intensidad del campo eléctrico.
• Por otro, la superficie que atraviesan dichas líneas de fuerza. Cada superficie plana se puede representar por medio de un vector $\overrightarrow{S}$ que se caracteriza porque:
  • $\overrightarrow{S}$ es siempre perpendicular a dicha superficie.
  • El módulo de $\overrightarrow{S}$ equivale al área de la superficie.

Para calcular el flujo eléctrico consideraremos varios casos:

• Campo eléctrico uniforme
  • Superficie plana perpendicular al campo eléctrico.
  • Supercicie plana no perpendicular al campo eléctrico.
• Campo eléctrico no uniforme
  • Superficie cualquiera abierta.
  • Superficie cualquiera cerrada.

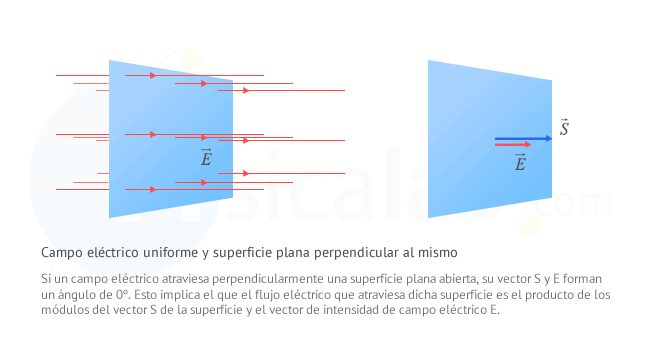
Flujo eléctrico de un campo eléctrico uniforme a través de una superficie plana perpendicular

Si nos atenemos a la definición de flujo eléctrico, cuando disponemos de un campo eléctrico uniforme $\overrightarrow{E}$ y una superficie $\overrightarrow{S}$, el flujo eléctrico (Φ_E) se puede calcular por medio de la siguiente expresión:

$${\Phi }_E=\overrightarrow{E}·\overrightarrow{S}$$

Si consideramos que la superficie es perpendicular al campo eléctrico (es decir, S y E forman un angulo de 0º entre ellos), aplicando la definición de producto escalar obtenemos que:

$${\Phi }_E=\overrightarrow{E}·\overrightarrow{S}=E·S·\cos 0 =E·S$$

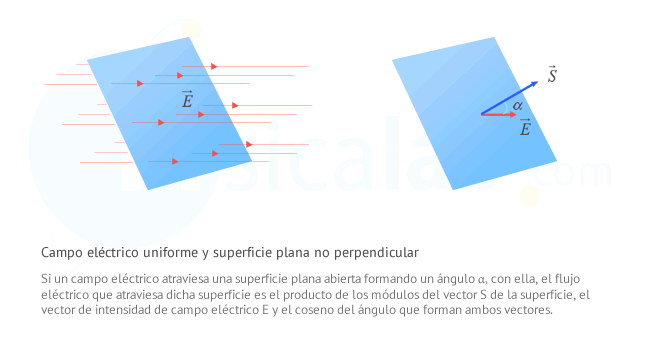
Flujo eléctrico de un campo eléctrico uniforme a través de una superficie plana no perpendicular

En este caso, el ángulo (α) que forman el vector $\overrightarrow{E}$ y el vector $\overrightarrow{S}$ no es 0, por tanto el flujo eléctrico dependerá de dicho ángulo:

$${\Phi }_E=\overrightarrow{E}·\overrightarrow{S}=E·S·\cos \alpha$$

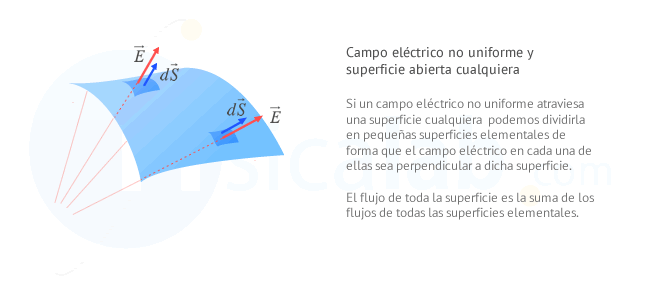
Flujo eléctrico de un campo eléctrico no uniforme a través de cualquier tipo de superficie abierta.

Lo más común es que los campos eléctricos no sean uniformes y las superficies no sean planas. En este caso, para calcular el flujo eléctrico es necesario dividir la superficie en pequeñas superficies elementales (d$\overrightarrow{S}$), cuyo carácter infinitesimal nos permita considerar que $\overrightarrow{E}$ en cada una de esas superficies elementales es constante. De esta forma, podemos definir el flujo que atraviesa cada superficie elemental de la siguiente forma:

$$d\Phi =\overrightarrow{E}·d\overrightarrow{S}$$

Una vez conocido el flujo que atraviesa cada superficie elemental, el flujo total que atraviesa toda la superficie será la suma de todos esos diferenciales de flujo.

Flujo eléctrico de un campo eléctrico no uniforme a través de cualquier tipo de superficie cerrada.

Basándonos en el flujo de campo eléctricos no uniformes que atraviesan superficies abiertas, es posible deducir que si disponemos de una superficie cualquiera cerrada, el flujo en dicha superficie se puede obtener como la suma de los flujos de cada una de las superficies abiertas que constituyen dicha superficie.