Teorema de Gauss

La ley de Gauss y el flujo eléctrico

La ley de Gauss, también conocida como teorema de Gauss fué enunciada por el matemático alemán Karl Friederich Gauss (1777-1855). Dicho matemático determinó en esta ley una relación entre el flujo eléctrico que atraviesa una superficie cerrada y la carga eléctrica que se encuentra en su interior.

Si observas con atención la expresión anterior puedes deducir facilmente que el flujo eléctrico no depende de la forma de la superficie cerrada, tan solo de la carga que posee en su interior y de la constante dieléctrica del medio.

Aplicaciones de la ley de Gauss

Aunque a la hora de calcular el campo eléctrico generado por ciertas superficies cargadas es posible hacer uso de la ley de Coulomb, en muchas ocasiones resulta más sencillo utilizar el teorema de Gauss sobre el flujo eléctrico. Para ello es común seguir los siguientes pasos:

1. Se escoge una superficie cerrada perpendicular al campo eléctrico y cuya área sea conocida para nosotros. Esta superficie recibe el nombre de superficie gaussiana y deberá envolver a la superficie que genera el campo.

2. Se aplica la expresión general del flujo eléctrico para cualquier tipo de superficie.

$${\Phi }_E={\oint }_S\overrightarrow{E}·d\overrightarrow{S}$$

3. El valor obtenido en el punto anterior se iguala a la expresión del teorema de Gauss.

$${\Phi }_E= \frac{Q}{\epsilon }$$

En concreto puedes estudiar la aplicación de esta estrategia en los siguientes casos:

• El campo creado por una esfera uniformemente cargada
• El campo creado por una lámina plana uniformemente cargada
• El campo creado por un hilo cargado uniformemente

Comprobación de la ley de Gauss. Una esfera con una carga en su interior.

El caso más simple para calcular el flujo eléctrico es el del campo creado por una carga q contenida en una esfera de radio r. Tal y como estudiamos en el apartado de intensidad del campo eléctrico, la intensidad del campo eléctrico generado por una carga se obtiene por medio de la siguiente expresión:

$$E=\frac{q}{4·\pi ·\epsilon ·r^2}$$

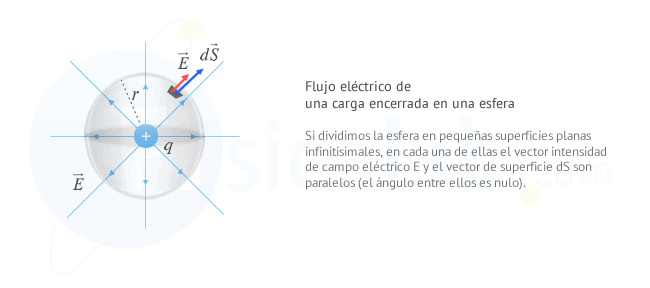
En este caso, como en cada punto de la esfera se cumple que $\overrightarrow{E}$ y $d\overrightarrow{S}$ son paralelos, el flujo a través de la superficie esférica es:

$${\Phi }_E={\oint }_S\overrightarrow{E}·d\overrightarrow{S} = {\oint }_{S}E·dS·\cos 0 = E{\oint }_{S}dS = E·S$$

Dado que la superficie de una esfera es S = 4·π·r², entonces:

$${\Phi }_E=\frac{q}{\cancel{4}·\cancel{\pi }·\epsilon ·\cancel{r^2}}·\cancel{4}·\cancel{\pi }·\cancel{r^2} =\frac{q}{\epsilon }$$

Probablemente ya te habrás dado cuenta que independientemente del radio r que posea la esfera el flujo eléctrico es el mismo, pero no solo eso. Si observas la siguiente figura puedes darte cuenta de que independientemente de la figura que empleemos, todas ellas poseen el mismo flujo eléctrico cuando contienen a q en su interior.