Producto Escalar de Vectores
Representación Gráfica del Producto Escalar
El producto escalar de un vector
donde
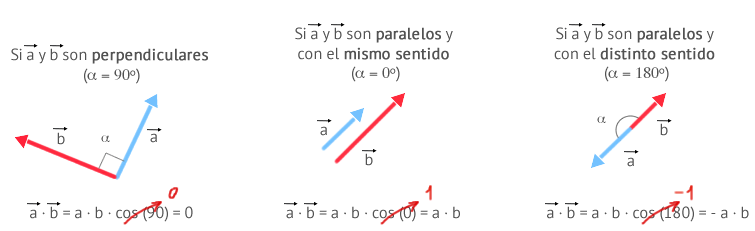
El cálculo del producto escalar de estos dos vectores se simplifica cuando estos son perpendiculares o paralelos entre si:
- Si son perpediculares, el ángulo forma 90º y el producto es 0
- Si son paralelos, tenemos dos posibilidades:
- Si tienen el mismo sentido, el producto escalar es la multiplicación de sus módulos
- Si NO tiene el mismo sentido, el producto escalar es la multiplicación de sus módulos añadiéndole el signo negativo.
Interpretación Geométrica del Producto Escalar
El producto escalar de dos vectores
Representación Analítica del Producto Escalar
El producto escalar de dos vectores
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
