Varios ejemplos de suma de fuerzas
Enunciado
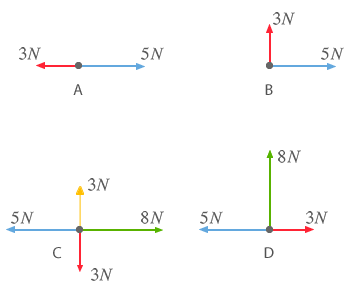
¿Sabrías determinar la fuerza resultante en cada uno de los siguientes casos?
Solución
Teniendo en cuenta lo estudiado en el apartado de suma de fuerzas concurrentes, vamos a determinar la fuerza resultante en cada caso. Cuando dispongas de varias fuerzas para sumar, lo ideal es que obtengas fuerzas resultantes parciales, sumando siempre de 2 en 2 fuerzas que posean la misma dirección hasta que te sea posible.
Caso A
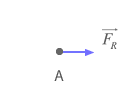
Ambas fuerzas concurrentes tienen la misma dirección aunque sentido contrario, por tanto el valor de la fuerza resultante será el valor absoluto de la resta de ambas y su dirección la de la mayor de ellas.
FR = | 5N - 3N | = 2 N con dirección horizontal y sentido hacia la derecha.
Caso B
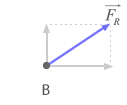
En este caso ambas fuerzas forman un ángulo de 90º, por tanto la fuerza resultante será la raíz de la suma de los cuadrados de ambas fuerzas.
Caso C
En este situación primero obtendremos las fuerzas resultantes parciales, en concreto calcularemos las fuerza resultante que se obtiene al sumar las fuerzas verticales (FV) e ignoraremos las horizontales.
FV = | 3 N - 3 N | = 0 N
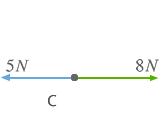
Podemos observar que las fuerzas verticales se anulan entre ellas y desaparecen. Por último, ya sólo nos queda calcular la resultante de estas dos fuerzas horizontales.
FR = | 8 N - 5 N | = 3 N
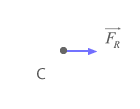
Caso D
Aquí procederemos como el caso C aunque calcularemos la fuerza resultante parcial en la horizontal (FH).
FH = | 5 N - 3 N | = 2 N
Tras esta operación el esquema de fuerzas queda de la siguiente forma:
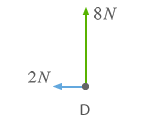
Ahora las dos fuerzas restantes forman un ángulo de 90º, por lo que:
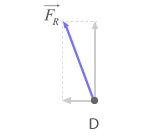
No hemos encontrado ninguna fórmula destacable en este ejercicio.
