Descomponiendo Fuerzas

En ocasiones, puede resultar muy útil descomponer una fuerza en dos fuerzas que tienen la misma dirección y sentido que los ejes del sistema de referencia que estemos empleando y cuyos efectos sumados sean equivalentes a la original.

Este procedimiento es muy común cuando, por ejemplo, debemos trabajar con el peso de un cuerpo que se encuentra sobre un plano inclinado. No te asustes, esto último lo estudiaremos más adelante.

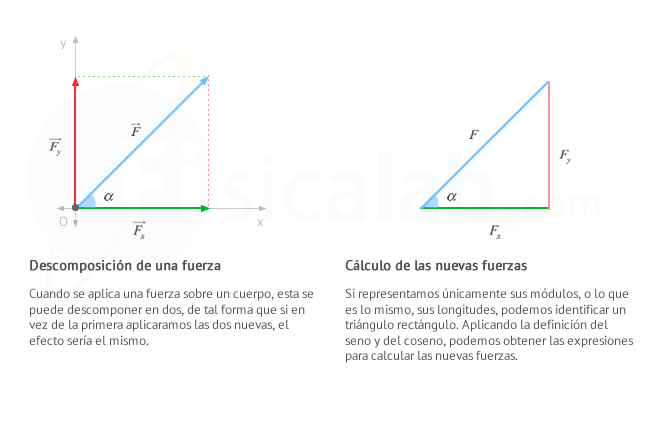
Para calcular el módulo de estas fuerzas que llamaremos F_x y F_y, podemos hacer uso de la definición del seno y del coseno:

$$F_x=F·\cos \left(\alpha \right) ; F_y=F·\sin \left(\alpha \right)$$

donde:

• F es el módulo de la fuerza original
• F_x es el módulo del vector que surge de la proyección del vector F en el eje x
• F_y es el módulo del vector que surge de la proyección del vector F en el eje y
• α es el menor ángulo entre F y el eje x

y para calcular la fuerza original F a partir de F_x y F_y utilizaremos la siguiente expresión que se obtiene aplicando el teorema de Pitágoras:

$$F=\sqrt{{F_x}^2+{F_y}^2}$$