Energía Potencial Elástica
Energía Potencial
La energía potencial es, junto con la energía cinética, el otro tipo de energía mecánica que pueden tener los cuerpos. A diferencia de la energía cinética, la energía potencial está asociada a la posición que tienen los cuerpos, y no a su movimiento.
Definimos la energía potencial como aquella que poseen los cuerpos por el hecho de encontrarse en una determinada posición en un campo de fuerzas.
Existen distintos tipos de energía potencial. En este apartado vamos a estudiar la energía potencial elástica. ¿Empezamos?
La Energía de los Muelles
¿Has jugado alguna vez al pinball? Para poner la bola en juego es necesario que comprimas el lanzador. Una vez comprimido, puedes mantenerlo en esa posición todo el tiempo que desees. La bola permanecerá en reposo. Sin embargo, una vez liberado, el lanzador (un muelle), transforma el estado de reposo de la bola, y esta se pone en movimiento. El resto depende de tu habilidad y tu suerte para evitar que la pelota caiga del tablero de juego. En cualquier caso, lo importante es señalar que el muelle deformado cuenta con una energía (capacidad para producir un trabajo, una transformación) por el hecho de encontrarse desplazado (comprimido o estirado) respecto a su posición de equilibrio.
Definimos la energía potencial elástica como aquella que adquieren los cuerpo sometidos a la acción de fuerzas elásticas o recuperadoras. En el caso de un cuerpo unido a un muelle su valor viene dado por:
Donde:
- Ep: Es la energía potencial del cuerpo. Su unidad de medida en el Sistema Internacional es el Julio (J)
- k: Constante elástica del muelle. Depende el propio muelle en sí, cuanto mayor es su valor, más trabajo cuesta estirar el muelle. Su unidad de medida en el Sistema Internacional es Newton por metro (N/m)
- x: Distancia hasta la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m)
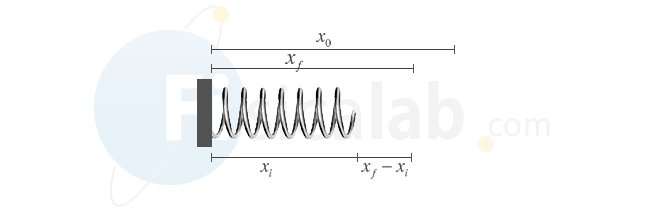
Observa como x es la distancia a la posición de equilibrio. Presta mucha atención en los problemas a dónde se sitúa el origen de coordenadas para distinguir claramente la posición inicial xi del muelle, la posición final xf , su posición de equilibrio x0 y la distancia a la posición de equilibrio x.
¿Cómo se obtiene la fórmula de la Energía Potencial Elástica?
Para obtener el valor de la energía potencial elástica podemos razonar de la siguiente manera.
- Vamos a comprimir o estirar un muelle desde su posición de equilibrio (x1 = 0) a posición una posición x2 = x. Consideraremos que el muelle no tiene energía inicial (E1 = 0) por encontrarse en su posición de equilibrio
- Para comprimir o estirar el muelle hemos de ejercer una fuerza igual en magnitud pero de sentido contrario a la ley de Hooke.
- La fuerza ejercida es variable, siendo prácticamente nula al principio y aumentando a medida que aumenta x
-
Para calcular el trabajo ejercido por nosotros sobre el muelle, calculamos el área del triángulo limitado por la curva.
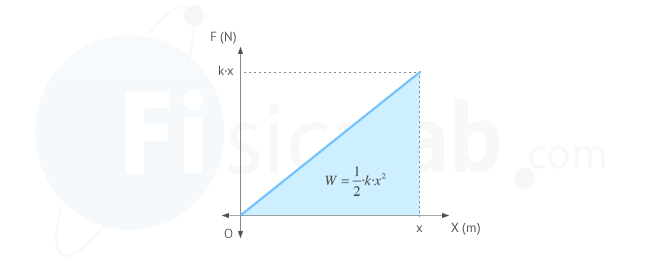
-
El muelle, sobre el que hemos realizado el trabajo, ha adquirido energía. Considerando que el trabajo que realiza una fuerza sobre un cuerpo es igual a su variación de energía y que el cuerpo al encontrarse en la posición de equilibrio x = 0 no tenía energía, nos queda que de modo que
Trabajo Realizado por la Fuerza Elástica
Podemos hallar el trabajo realizado por la fuerza elástica o restauradora a través de su relación con la energía potencial elástica.
El trabajo realizado por las fuerzas elásticas es igual a la variación negativa de la energía potencial
¿Cómo se obtiene el trabajo realizado por la fuerza elástica?
Si queremos calcular el trabajo realizado por la fuerza elástica sobre un muelle comprimido que se encuentra en una posición xi y se desplaza a una posición xf , ambas a la izquierda del punto de equilibrio x0, podemos ayudarnos de la siguiente figura y los siguientes razonamientos:
- Será la fuerza elástica la que realizará el trabajo sobre el muelle tratando de llevarlo a su posición de equilibrio.
- La fuerza de recuperación elástica que actúa sobre el cuerpo sigue la ley de Hooke.
- Podemos calcular la fuerza en la posición inicial xi según la siguiente expresión
- Podemos calcular la fuerza en la posición final xf según la siguiente expresión
- Nos resta el cálculo del trabajo realizado por la fuerza elástica (variable). Tenemos varias opciones:
- Podemos calcular el área bajo la fuerza elástica en la gráfica fuerza - desplazamiento. Este procedimiento ya lo hemos señalado en el punto anterior
-
Podemos seguir un razonamiento similar al aplicado en el teorema de Merton para el cálculo de la velocidad media: Calcular la fuerza elástica promedio y usar este valor para el cálculo del trabajo. El valor del trabajo de la fuerza elástica (variable) tendrá igual valor que el que lleve a cabo esta fuerza constante de valor promedio.
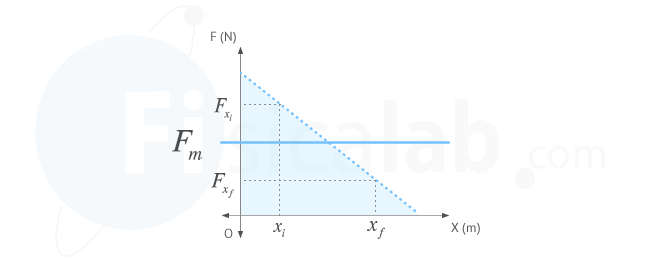
El valor de la fuerza elástica promedio:
Con todo lo anterior nos queda
Como puedes observar, el trabajo realizado por las fuerzas elásticas es igual a la variación negativa de la energía potencial.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
