Equilibrio en los Sólidos

En muchas ocasiones leerás u oirás que un cuerpo se encuentra en equilibrio. En la Física el concepto de equilibrio está fuertemente asociado a las fuerzas y sus momentos y por ende a lo que se conoce como centro de gravedad. Para responder a todas estas cuestiones, a lo largo de este apartado nos centraremos en estudiar:

¿Qué se entiende por equilibrio?
¿Cómo actúan las fuerzas paralelas sobre los cuerpos sólidos?
¿Qué es el centro de gravedad de un cuerpo (cdg) ?
Tipos de Equilibrio

¿Qué es el equilibrio?

Como hemos estudiado en apartados anteriores, todas las fuerzas que actúan sobre un cuerpo pueden ser sustituidas por una única fuerza denominada fuerza resultante que posee el mismo efecto que las anteriores. De igual manera, el momento de cada una de ellas puede ser sustituido por un único momento resultante. Recuerda que si bien la fuerza resultante es la responsable de la variación de la velocidad de traslación del cuerpo, el momento resultante es el responsable de la variación de la velocidad con la que rota.

Un cuerpo se encuentra en equilibrio de traslación cuando la fuerza resultante, $\vec{F}$ , que actúa sobre él es cero. De igual forma, un cuerpo se encuentra en equilibrio de rotación cuando el momento resultante de las fuerzas aplicadas, $\vec{M}$ , es cero.

$\vec{F} = 0 \vec{M} = 0$

Fuerzas paralelas sobre un sólido

Cuando dos o más fuerzas paralelas actúan sobre un sólido:

El valor de la fuerza resultante es la suma algebraica del valor de todas las fuerzas que actúan sobre el sólido, considerando positivas las que poseen un sentido hacia un lado y negativas las que poseen el sentido contrario al elegido como positivo.
El valor del momento resultante es la suma algebraica de los momentos de todas las fuerzas aplicadas sobre el sólido, considerando positivos aquellos momentos que tienden a provocar un giro del cuerpo en el sentido contrario de las agujas del reloj y negativos si se tiende a producir un giro en el sentido de las agujas del reloj.
El punto de aplicación de la fuerza resultante es aquel en el que el se produce el mismo momento respecto de cualquier punto del sólido.

Para equilibrar el sistema, tan solo es necesario aplicar una fuerza de igual valor aunque de sentido contrario que la fuerza resultante. Dicha fuerza recibe el nombre de fuerza equilibrante.

Con el fín de entender un poco mejor los puntos que acabamos de exponer, vamos a estudiar el caso específico de dos fuerzas paralelas aplicadas sobre una barra rígida. ¿Estás preparado?

Fuerzas paralelas con el mismo sentido

Si se aplican dos fuerzas paralelas ${\vec{F}}_{1}$ y ${\vec{F}}_{2}$ que poseen el mismo sentido sobre una barra el valor de la fuerza resultante, $\vec{F}$ , será siempre la suma de los valores de ambas: F = F₁+ F₂. Por otro lado, cada una de ellas creará un momento de valor M₁ = -F₁· d₁ y M₂= F₂· d₂. Observa que hemos considerado M₁ como negativo ya que ${\vec{F}}_{1}$ intenta girar la barra en el sentido de las agujas del reloj y M₂ como positivo ya que ${\vec{F}}_{2}$ intenta girarla en el sentido contrario de las agujas del reloj. El hecho de que situemos el origen O de las distancias sobre el punto de aplicación de la fuerza resultante no es casual, ya que en dicho punto la distancia es nula, lo que hace que el valor del momento, $\vec{M}$ , de la fuerza resultante $\vec{F}$ sea nulo. M = F · 0 = 0 N · m.

Teniendo en cuenta que la suma algebraica del momento de las fuerzas individuales debe ser igual al momento de la resultante:

$- F_{1} \cdot d_{1} + F_{2} \cdot d_{2} = F \cdot 0 \Rightarrow F_{1} \cdot d_{1} = F_{2} \cdot d_{2}$

Si observas detenidamente la ecuación anterior puedes deducir que el punto de aplicación de la fuerza resultante siempre tiene que encontrarse entre las dos fuerzas ya que si no, nunca se podrían restar los momentos de F₁ y F₂ provocando que el momento de la fuerza resultante se anule.

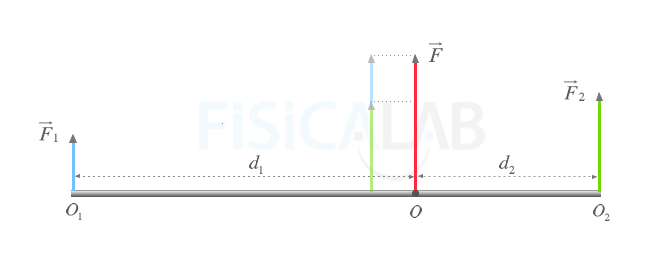
Dos fuerzas paralelas con el mismo sentido

En la figura se muestra una barra sólida sobre la que se aplican dos fuerzas. Dado que ambas tienen el mismo sentido, pueden ser sustituidas por una fuerza resultante cuyo valor que será la suma del valor de ambas. F = F₁ + F₂. Observa que el origen de la fuerza resultante siempre debe encontrarse entre ambas fuerzas.

Fuerzas paralelas con distinto sentido

Si se aplican dos fuerzas paralelas ${\vec{F}}_{1}$ y ${\vec{F}}_{2}$ que poseen distinto sentido sobre una barra, el valor de la fuerza resultante, $F$ , será siempre la suma de los valores de ambas aunque considerando una positiva y la otra negativa: F = F₁- F₂. Por otro lado, cada una de ellas creará un momento de valor M₁ = F₁· d₁ y M₂= -F₂· d₂. Observa que hemos considerado M₁ como positivo ya que ${\vec{F}}_{1}$ intenta girar la barra en el sentido contrario de las agujas del reloj y M₂ como negativo ya que ${\vec{F}}_{2}$ intenta girarla en el sentido de las agujas del reloj. El hecho de que volvamos a situar el origen O de las distancias sobre el punto de aplicación de la fuerza resultante no es casual, ya que en dicho punto la distancia es nula, lo que hace que el valor del momento, $\vec{M}$ , de la fuerza resultante $\vec{F}$ sea nuevamente nulo. M = F · 0 = 0 N · m.

Teniendo en cuenta que la suma algebraica del momento de las fuerzas individuales debe ser igual al momento de la resultante:

$F_{1} \cdot d_{1} - F_{2} \cdot d_{2} = F \cdot 0 \Rightarrow F_{1} \cdot d_{1} = F_{2} \cdot d_{2}$

Si observas detenidamente la ecuación anterior puedes deducir que el punto de aplicación de la fuerza resultante siempre tiene que encontrarse situada fuera de las dos fuerzas ya que si no, nunca se podrían restar los momentos de F₁ y F₂ provocando que el momento de la fuerza resultante se anule. Además dicho punto debe estar situado más próximo a la fuerza de mayor valor.

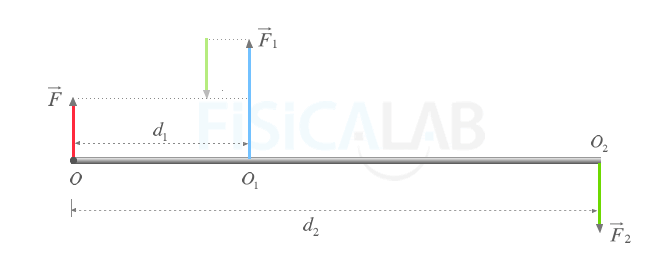
Dos fuerzas paralelas con distinto sentido

En la figura se muestra una barra sólida sobre la que se aplican dos fuerzas. Dado que ambas no tienen el mismo sentido, pueden ser sustituidas por una fuerza resultante cuyo valor que será la suma del valor de ambas considerando una de ellas negativa. F = F₁ - F₂. Observa que el origen de la fuerza resultante siempre debe encontrarse fuera de ambas fuerzas y más próxima a la fuerza de mayor valor.

Ejemplo

Demuestra que la fuerza resultante de dos fuerzas paralelas ( ${\vec{F}}_{1}$ y ${\vec{F}}_{2}$ ) con sentidos contrarios y aplicados sobre un sólido, se encuentra siempre más cerca de la fuerza de mayor valor.

Ver solución

Par de Fuerzas

Cuando dos fuerzas aplicadas sobre un cuerpo, por medio de una separación d, poseen el mismo valor, dirección y sentido opuesto reciben el nombre de par de fuerzas.

Si aplicamos un par de fuerzas sobre un sólido, el valor de la fuerza resultante será 0, ya que al ser paralelas y de sentido contrario ambas fuerzas se anulan. Sin embargo, el valor del momento resultante será la suma de las momentos de cada una de ellas:
$M = F \cdot d + F \cdot 0 \Rightarrow M = F \cdot d$

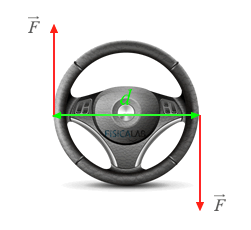
Par de Fuerzas

Se caracterizan porque la fuerza resultante de dichas pareja de fuerzas es cero, sin embargo posee un momento resultante que provoca una alteración en la velocidad de giro del cuerpo sobre el que se aplican.

Ejemplo

Determina el momento resultante de dos fuerzas palalelas y de sentido contrario de 30 N cada una aplicadas sobre los extremos de un volante de 25 cm de radio.

Ver solución

Centro de Gravedad

Los cuerpos extensos pueden considerarse como la unión de un conjunto de partículas con su propia masa y por tanto, su propio peso. El peso es una fuerza, por lo que es posible calcular la fuerza resultante de todas los pesos de esas partículas que lo componen ¿Verdad?. Pues bien, el punto de aplicación de ese peso/fuerza resultante es lo que se conoce como centro de gravedad.

El centro de gravedad (cdg) de un cuerpo es el punto de aplicación de la fuerza resultante de todos los pesos de cada una de las partes que conforman el cuerpo, de tal forma que se comporta como si todo su peso se encontrara concentrado en él.

Aunque pueda parecer extraño el centro de gravedad puede estar o no dentro del material que compone al cuerpo. Todo depende de la forma que posea. Por ejemplo, en una barra está dentro, pero en una esfera hueca está fuera. En cualquier caso resulta más o menos sencillo determinar su ubicación en sólidos simétricos y homogéneos.

El centro de gravedad en sólidos simétricos y homogéneos coincide con el centro de su simetría.

Tipos de Equilibrio

En base a como se comporta el cuerpo cuando se aparta de su posición de equilibrio, podemos distinguir tres tipos:

Equilibrio estable: Si apartamos el cuerpo de su posición de equilibrio este vuelve a su posición original debido a la aparición de un par de fuerzas.
Equilibrio Inestable. Si apartamos el cuerpo de su posición de equilibrio aparecen un par de fuerzas que provocan que se aparte aún más de su posición de equilibrio.
Equilibrio indiferente. Si cambiamos la posición del cuerpo este se seguirá encontrando en equilibrio al no generarse ningún momento sobre él.

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.