Palancas
La palanca es una máquina simple compuesta por una barra rígida situada sobre un punto de apoyo denominado fulcro. En el funcionamiento de la palanca intervienen tres fuerzas:
- Potencia, P. Se trata de una fuerza que aplicamos voluntariamente en una parte de la barra con el fin de vencer a otra fuerza denominada Resistencia. Su distancia con respecto al punto de apoyo sobre el fulcro se denomina brazo de potencia, Bp.
- Resistencia, R. Se trata de una fuerza ejercida sobre la palanca por un cuerpo que generalmente tratamos de mover o deformar mediante la Potencia. Su distancia con respecto al punto de apoyo sobre el fulcro se denomina brazo de resistencia, Br.
- Reacción Normal, N. Es la fuerza ejercida por el fulcro sobre la barra. Si consideramos que la barra no tiene masa, N se obtiene como la suma de las fuerzas P y R.
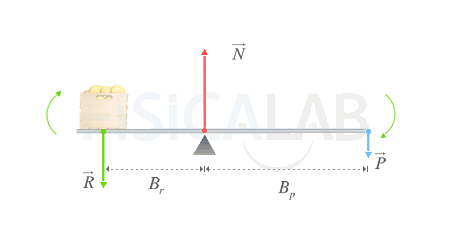
Palanca
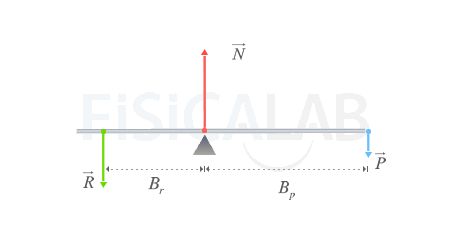
En la figura se muestra un tipo específico de palanca en equilibrio. Está conformada por una barra apoyada sobre un fulcro (triángulo) que le permite rotar sobre él. Observa que aplicando una potencia relativamente pequeña P en un extremo podemos igualar la resistencia R (cuyo valor es mayor que P y que en este caso coincide con el peso de una caja) dejando la máquina en reposo. Si aumentáramos el valor de P provocaríamos que la caja se levantara con relativo poco esfuerzo.
Ley de la Palanca
Cualquier palanca se encontrará en equilibrio de traslación cuando se cumpla que la fuerza resultante de todas las fuerzas que actúan sobre la barra sea nula:
Adicionalmente, la palanca se encontrará en equilibrio de rotación cuando se cumpla que el momento resultante sea nulo. Si consideramos el origen de coordenadas en el fulcro, el momento resultante en ese punto será nulo. Teniendo en cuenta la definición de momento:
Esta última expresión recibe el nombre de ley de la palanca.
La ley de la palanca establece que en cualquier palanca se cumple que el producto de la potencia P por la distancia de su brazo Bp es equivalente al producto de la resistencia Rp por la longitud de su brazo.
Clases de Palancas
Podemos distinguir tres tipos de palancas dependiendo del punto sobre el que se apliquen P y R: las palancas de primer género, segundo género y tercer género.
Primer género
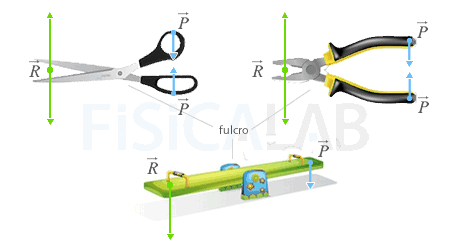
Palanca de Primer Género
Este tipo de palancas poseen el fulcro situado entre los puntos sobre los que se aplican las fuerzas P y R. Un ejemplo claro de este tipo de palancas son las tijeras, las balanzas, los alicates o las tenazas.
Segundo género
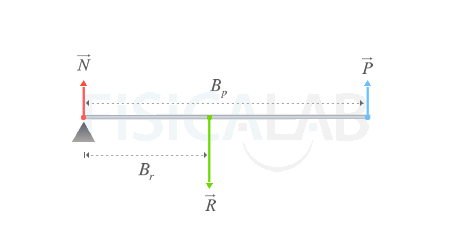
Palanca de Segundo Género
Este tipo de palancas poseen el punto de aplicación de R entre el fulcro y P. Ejemplos de este tipo de palancas son el cascanueces, la carretilla o el abre botellas.

Tercer género

Palanca de Tercer Género
El punto de aplicación de P se encuentra entre el fulcro y R. Ejemplos claros de este tipo de palancas son las pinzas o la caña de pescar.

Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
