Fuerza Gravitatoria

Sir Isaac Newton, durante su retiro en una granja de Woolsthorpe durante los años 1665-1666 elaboró la base de lo que hoy se conoce como la ley de gravitación universal, basándose en las leyes de Kepler sobre el movimiento de los planetas y los estudios de Galileo.

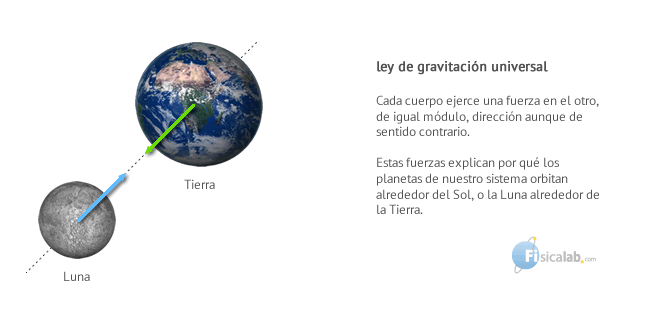
Esta ley establece que los cuerpos, por el simple hecho de tener masa, experimentan una fuerza de atracción hacia otros cuerpos con masa, denominada fuerza gravitatoria o fuerza gravitacional. Esta fuerza, explica entre otras muchas cosas, por qué orbitan los planetas.

De igual forma, el módulo de dicha fuerza se puede obtener mediante la siguiente ecuación:

$$F_g=G·\frac{M·m}{r^2}$$

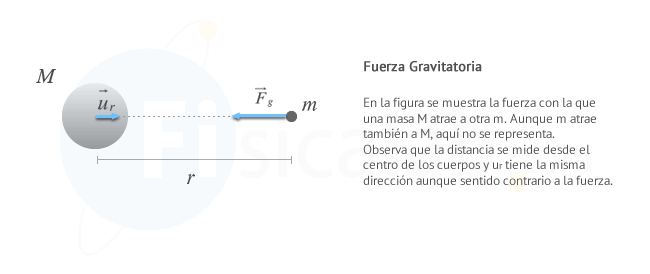
Ambas expresiones de la ley de la gravitación universal, únicamente sirven para masas puntuales y cuerpos esféricos, ya que estos se comportan como si toda su masa se concentrara en su centro. Por tanto, la distancia se mide desde sus centros.

Consecuencias de la ley de gravitación universal

La atracción que ejercemos sobre la Tierra

Las fuerzas gravitacionales, como fuerzas que son, obedecen el principio de acción reacción o tercera ley de Newton, por lo tanto:

¿Entonces por qué la Tierra no nos persigue cuando nos alejamos del suelo? Nuestra masa es muy inferior a la de la Tierra, por lo que cuando la fuerza gravitacional actúa sobre la Tierra y sobre nosotros, ella se mueve extremadamente poco hacia nosotros (despreciable) y nosotros mucho hacia ella. No es lo mismo aplicar la misma fuerza a un carro vacio que un lleno y que posee más masa. Obviamente el vacío se moverá más rápido.

La gravedad no depende de la masa de los cuerpos

Si un cuerpo de masa m se encuentra a una altura h sobre la superficie de la Tierra, la fuerza gravitacional que actúa sobre él es:

$$F_g=G·\frac{M_T·m}{{\left(r_T+h\right)}^2}$$

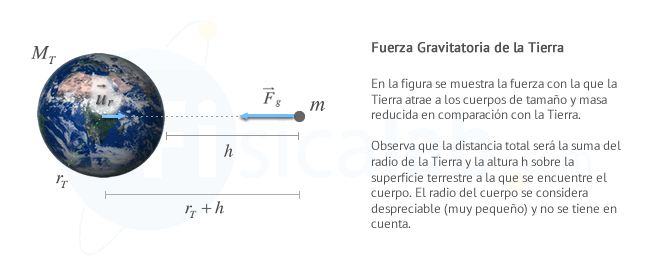
De acuerdo con la segunda ley de Newton, esta fuerza gravitatoria imprimirá una aceleración en el cuerpo, de tal forma que:

$$\begin{gathered} F_g=G·\frac{M_T·\cancel{m}}{{\left(r_T+h\right)}^2}=\cancel{m}·a \Rightarrow \\ a=G·\frac{M_T}{{\left(r_T+h\right)}^2} \end{gathered}$$

Si consideramos que la altura es despreciable con respecto al valor del radio de la Tierra, podemos simplificar la expresión de la siguiente forma:

$$a=G·\frac{M_T}{{r_T}^2}$$

Esta aceleración es lo que comúnmente llamamos gravedad y representamos con la letra g. (g=9.8 m/s²).

$$g=G·\frac{M_T}{{r_T}^2}$$

Expresada de forma vectorial, la gravedad se calcula de la siguiente forma:

$$\overrightarrow{g}=-G·\frac{M_T}{{r_T}^2}·{\overrightarrow{u}}_r$$