El Sólido Rígido
Un sólido rígido es un cuerpo formado por varias partículas puntuales que guardan distancias constantes entre sí. Es un modelo que usamos en dinámica para estudiar los cuerpos en aquellos casos en los que no podemos suponer que toda su masa se concentra en un único punto. En este apartado estudiaremos:
- Qué representa la magnitud masa
- Las características que tiene el sólido rígido
- Sus dos tipos fundamentales
- Sus movimientos característicos
¿Qué es la masa?
Observa esta escena en la que el intrépido Indiana Jones corre perseguido por una roca gigante. ¿Por qué huir, en lugar de intentar pararla? ¿Crees que Indy correría si la bola fuese de cartón, en lugar de roca pesada?
Desde el punto de vista cinemático, tanto la roca como la hipotética bola de cartón se comportan igual, es decir, tienen la misma velocidad. Sin embargo el movimiento de la bola se caracteriza, no sólo por su velocidad, sino también por su masa, tal y como dijimos cuando presentamos la cantidad de movimiento o momento lineal. A mayor masa y a mayor velocidad, más inercia tiene la bola, es decir, mayor dificultad en detenerla. De ahí que la mejor opción del doctor Jones sea la huida.
Gracias a la magnitud masa, podemos estudiar la dificultad que presentan los cuerpos para variar su velocidad, es decir, su inercia. Por eso, a esta masa también se la conoce como masa inercial.
La masa es una medida cuantitativa (numérica) de la inercia de un cuerpo.
El modelo del sólido rígido
Hasta ahora hemos considerado que los cuerpos se encuentran en un sólo punto del espacio, y tienen una masa determinada. Es lo que denominámos masa puntual, punto material o partícula puntual. No hemos tenido en cuenta las dimensiones del cuerpo en movimimiento. La realidad es que los cuerpos se componen de millones de partículas. Por ello podemos considerar un cuerpo real como una suma de puntos materiales. El caso más simple de sistema formado por varios puntos materiales es el del sólido rígido.
Un sólido rígido es cualquier cuerpo formado por varios puntos materiales cuyas distancias mutuas permanecen constantes, incluso bajo la acción de fuerzas exteriores.
El sólido rígido es un caso ideal, es decir, se trata de un modelo, una abstracción de la realidad que resulta útil para estudiar ciertos tipos de cuerpos.

En el modelo del sólido rígido, las fuerzas interiores de cohesión de las partículas que forman el sólido se suponen tan fuertes que los cuerpos son indeformables. Estas fuerzas de cohesión se anulan dos a dos por la tercera ley de la dinámica y por ello no es necesario tenerlas en cuenta a la hora de resolver la mayoría de nuestros problemas, sin embargo, es importante que recuerdes que, gracias a ellas, la forma del sólido se mantiene constante incluso bajo la acción de fuerzas externas altas. Estas fuerzas pueden hacer que el sólido se mueva (se traslade o rote), pero, idealmente, nunca se deformará.
Si, como hemos visto, el sólido rígido es un modelo para estudiar los cuerpos reales, ¿cuándo podemos usarlo?
- En la realidad todos los cuerpos se deforman cuando se aplican fuerzas sobre ellos. Sin embargo, podemos emplear el modelo cuando las deformaciones que se producen son despreciables frente a las dimensiones del sistema
- Además, podemos emplear el modelo cuando las dimensiones del cuerpo que se mueve no son despreciables frente a las de la trayectoria descrita. En caso contrario, podríamos estudiar el cuerpo como una masa puntual
Finalmente, para caracterizar el sólido rígido es muy importante el estudio su centro de masas.
Tipos
Existen dos grandes categorías de sólido rigido:
-
Sólido rígido discreto: Se compone de un número determinado de partículas distinguilbles. Dichas partículas se encuentran en posiciones no contiguas

-
Sólido rígido continuo: Se compone de un número infinito de partículas no distinguibles. Dichas partículas se encuentran en posiciones infinitamente próximas entre sí

Movimientos
Cuando aplicamos una fuerza sobre el sólido rígido, este se mueve, conservando su forma. Cualquier movimiento del sólido rígido se puede descomponer en dos clases: traslación y rotación.
- Traslación: Se produce cuando todas las partículas del cuerpo describen trayectorias paralelas. Cuando aplicas una fuerza en el centro de masas de un cuerpo, se produce un movimiento de traslación pura.
- Rotación: Existe un eje de rotación, real o imaginario, en torno al cual las partículas describen circunferencias. Los efectos de una fuerza sobre la rotación de un cuerpo están asociados a los momentos que genera dicha fuerza en el cuerpo
En la naturaleza abundan ejemplos de ambos tipos de movimiento que, en la mayoría de los casos, se producen de manera combinada. En tal caso decimos que pueden ser:
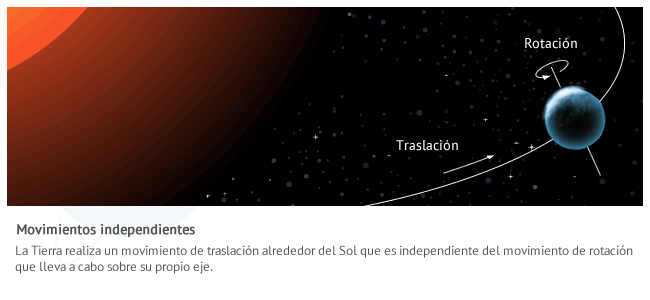
- Independientes. No hay relación entre la rotación y la traslación del cuerpo. Por ejemplo la Tierra en su recorrido alrededor del Sol
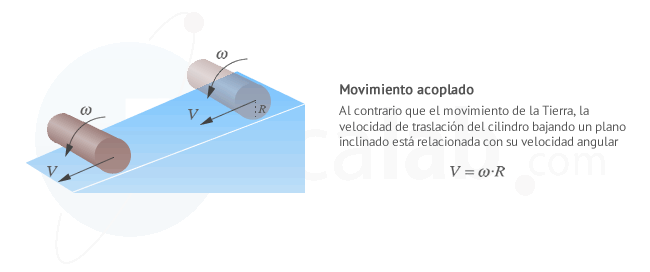
- Acoplados: La velocidad de traslación y rotación se encuentran relacionadas. Por ejemplo un cilindro rodando en un plano inclinado
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
