Centro de Masas
El centro de masas representa el punto que tenemos que estudiar cuando, en lugar de una partícula puntual, tenemos un cuerpo real, formado por varias de ellas. En este apartado estudiaremos:
- Para qué se usa el centro de masas
- Su posición
- Su velocidad
- Su aceleración
- Su momento lineal
- Las diferencias que podemos encontrar respecto al centro de gravedad
Adicionalmente, puede que te interese profundizar en el concepto de sólido rígido.
El centro de masas
Cuando un cuerpo se encuentra en movimiento, por ejemplo, al lanzar un lápiz al aire, todas sus partículas se mueven a la vez, aunque con distintas trayectorias. Para caracterizar la traslación del lápiz en su conjunto, sin embargo, nos basta con estudiar qué ocurre en un solo punto del mismo: su centro de masas. Este será el que determine su velocidad, su trayectoria, etc.

El centro de masas representa el punto en el que suponemos que se concentra toda la masa del sistema para su estudio. Es el centro de simetría de distribución de un sistema de partículas.
Recuerda que en dinámica podemos usar el modelo del sólido rígido, frente al de partícula puntual, cuando las dimensiones del cuerpo que estamos estudiando no son despreciables frente a la trayectoria que describe. En este apartado vamos a estudiar las magnitudes cinemáticas y dinámicas referidas al centro de masas de un sólido rígido discreto, es decir, aquel en el que se pueden distinguir las partículas que lo componen.
Posición
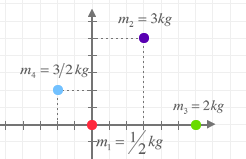
Si conocemos la posición de cada partícula del sólido, podemos determinar la de su centro de masas.
La posición del centro de masas de un sólido rígido discreto viene dada por:
Donde:
- n : Número de partículas del sistema
- mtotal , mi : Masa total del cuerpo y de cada partícula respectiva que compone el sistema. Su unidad de medida en el Sistema Internacional es el kilogramo ( kg )
Observa que en un espacio en tres dimensiones podemos escribir:

Velocidad
La velocidad instantánea, o simplemente velocidad, del centro de masas se puede obtener derivando respecto al tiempo la expresión de su posición
La velocidad del centro de masas de un sólido rígido discreto viene dada por:
Donde:
- mtotal , mi : Masa total del sólido y de cada una de las partículas que lo componen. Su unidad de medida en el Sistema Internacional es el kilogramo ( kg )
Aceleración
La aceleración instantánea, o simplemente aceleración, del centro de masas se puede obtener derivando respecto al tiempo la expresión de su velocidad
La aceleración del centro de masas de un sólido rígido discreto viene dada por:
Donde:
- mtotal , mi : Masa total del sólido y de cada una de las partículas que lo componen. Su unidad de medida en el Sistema Internacional es el kilogramo ( kg )
Momento lineal
En el sólido rígido existen dos tipos de fuerzas:
- Fuerzas internas de cohesión de las partículas. Hacen que el sólido se mantenga rígido en todo momento
- Fuerzas exteriores. De existir, son las responsables de que el cuerpo en su conjunto varíe su estado de reposo o movimiento. Pueden actuar sobre cualquiera de sus partículas y sus efectos se sentirán sobre todo el cuerpo
De acuerdo a la segunda ley de Newton, la resultante de las fuerzas que actúan sobre un cuerpo es proporcional a la variación de su momento lineal. Pues bien, en el caso del sólido rígido discreto, dicho principio se aplica a la resultante de las fuerzas exteriores, pues las fuerzas interiores de cohesión de las partículas se anulan dos a dos, por la tercera ley de Newton.

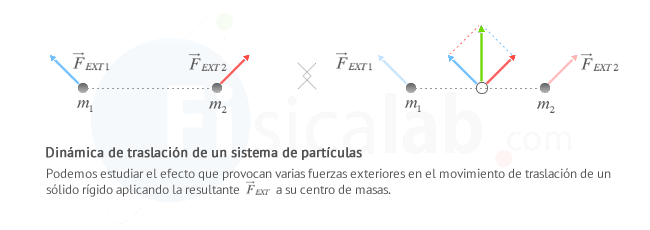
Bajo la influencia de fuerzas exteriores que actúan sobre un sistema de partículas, su centro de masas se mueve como si toda la masa de aquel estuviera concentrada en este. Este enunciado se recoge en la ecuación fundamental de la dinámica de traslación de un sistema de partículas:
Donde:
- mtotal : Es la masa total del cuerpo. Se puede calcular como la suma de las masas de cada partícula que compone el sólido. Su unidad de medida en el Sistema Internacional es el kilogramo ( kg )
Este teorema reduce el estudio del movimiento de un sistema de partículas al de una sola, concentrada en su centro de masas. Se trata, no obstante, de una descripción parcial, ya que describe el movimiento de traslación del sólido, de su centro de masas, pero no dice nada acerca del movimiento de las partículas respecto de dicho centro, es decir, de la rotación del cuerpo.
Por otro lado, podemos relacionar el momento lineal de cada partícula que compone el sistema con el momento lineal del centro de masas.
El momento lineal
Comprobaciónes
Si derivamos la posición del centro de masas respecto al tiempo, para obtener la velocidad del movimiento, nos queda:
Donde debes recordar que el momento lineal de un sistema de partículas
Si derivamos ahora nuevamente respecto al tiempo, llegamos a la ecuación fundamental de la dinámica de traslación de un sistema de partículas:
Diferencia con el centro de gravedad
El centro de gravedad de un cuerpo es otro punto que se suele utilizar para estudiar el comportamiento de un sistemas de partículas. En concreto, es el punto al que aplicamos el vector peso del sistema, que es la resultante del vector peso de cada una de las partículas. Para que exista centro de gravedad, debe existir un campo gravitatorio. Sino, sólo existe centro de masas.
En general, el centro de gravedad no coincide con el centro de masas por que el campo gravitatorio no es uniforme. Sin embargo, en la mayoría de los problemas que te encontrarás, puedes suponer el campo gravitatorio constante y por tanto los dos puntos coincidirán.
Conclusión
Cuando las dimensiones del cuerpo estudiado son equiparables a las de la trayectoria que describe no podemos considerar el cuerpo como una partícula puntual para describir completamente su movimiento, sin embargo si que podemos describir su movimiento de traslación a partir del estudio de su centro de masas, ignorando las posibles rotaciones o vibraciones de sus infinitas partículas respecto a él.
Finalmente, una puntualización. En este apartado hemos estudiado cómo determinar distintas magnitudes físicas del centro de masas de un sistema formado por varias partículas distinguibles, es decir, que constituyen un sólido rígido discreto. El cálculo para los sólidos rígidos continuos queda fuera del alcance de este nivel.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.