Momento Angular

El momento angular es una magnitud vectorial que utilizamos en física para caracterizar el estado de rotación de los cuerpos. En este apartado trataremos los siguientes puntos:

• El momento angular de una partícula puntual: Lo utilizamos para caracterizar el estado de rotación de un punto o de un cuerpo que se pueda tratar como tal. Recuerda que esto sucede cuando las dimensiones del cuerpo son despreciables frente a las de la trayectoria de su movimiento
• Qué es el momento de inercia de una partícula y como se relaciona con el momento angular
• El momento angular de un sistema de partículas: Lo utilizamos, por ejemplo, para caracterizar el estado de rotación del sólido rígido
• Cuándo varía el momento angular
• Bajo qué condiciones se conserva

Adicionalmente, puede que te interese profundizar en el concepto de sólido rígido.

Antes de comenzar a tratar el momento angular en sí, debemos hablar del convenio que seguimos cuando tratamos las magnitudes angulares como vectores.

Magnitudes angulares vectoriales

Para poder describir con precisión y coherencia cómo se comportan los cuerpos cuando rotan hemos de presentar como vectores las magnitudes angulares cinemáticas. Para ello debemos llegar a algún tipo de acuerdo sobre la dirección y sentido que presentarán estás magnitudes, ya que estos nos son tan claros como el caso de la velocidad lineal, por ejemplo, o la fuerza que se ejerce sobre una partícula.

Consideraremos como punto de aplicación el centro geométrico y como dirección el eje de giro. El sentido del vector varía en función de la magnitud que consideramos.

Además, podemos relacionar las magnitudes angulares anteriores con las lineales velocidad instantánea y aceleración tangencial a través de las siguientes expresiones:

$$\overrightarrow{v}=\overrightarrow{\omega }\times \overrightarrow{R}$$ 

$${\overrightarrow{a}}_t=\overrightarrow{\alpha }\times \overrightarrow{R}$$

Momento angular de un punto material

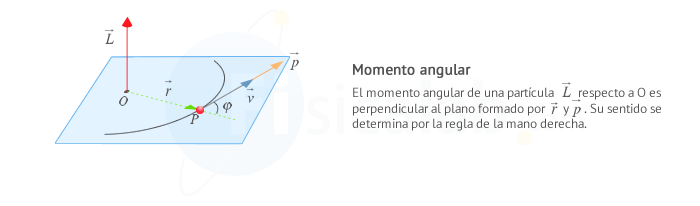
El momento angular de un punto material se define a partir de un vector de posición y una partícula puntual en movimiento, esto es, con cierta velocidad instantánea. Observa que no es una magnitud propia del cuerpo, sino que depende del punto de referencia que se escoja. Su significado físico tiene que ver con la rotación: El momento angular caracteriza el estado de rotación de un punto material, del mismo modo  que el momento lineal caracteriza el estado de traslación lineal. Para entender bien esta idea, vamos a presentar una nueva magnitud: el momento de inercia.

Momento de Inercia

Podemos definirlo para el caso concreto de los movimientos circulares.

Podemos relacionar el momento de inercia de una partícula puntual en movimiento circular con su momento angular. Recuerda que el vector de posición de un cuerpo que gira en movimiento circular respecto al centro de giro de dicho movimiento y el vector velocidad forman un ángulo de 90º. Entonces, a partir de la expresión del momento angular podemos escribir:

$$\begin{gathered} L=r·p·\sin \left(90º\right)=r·p=r·m·v\underset{\left[1\right]}{=}r·m·\left(\omega ·r\right)=m·r^2·\omega \\ I=m·r^2\Rightarrow L=I·\omega \\ \left[1\right]v_i={\omega }_i·r_i \end{gathered}$$ 

Quedando en notación vectorial:

$$\boxed{\overrightarrow{L}=I·\overrightarrow{\omega }}$$

Donde hemos tenido en cuenta que la velocidad angular se considera un vector axial que es perpendicular al plano de giro y con el sentido que determine la regla de la mano derecha.

Observa la analogía que hay entre la expresión anterior y $\overrightarrow{p}=m·\overrightarrow{v}$ . Como se puede deducir de las expresiones, el papel que juega el momento inercial I en el momento angular $\overrightarrow{L}$  es análogo al que juega la masa inercial m en el momento lineal $\overrightarrow{p}$ . En los movimientos rectilíneos, cuanto mayor sea la masa de un cuerpo, más difícil es modificar su momento lineal. En los movimientos circulares, cuanto mayor sea el momento inercial I, más resistencia hay a modificar el estado de rotación (el momento angular).

Momento angular y momento de inercia de un sólido rígido

También podemos considerar un sólido rígido en rotación. En este caso, queremos caracterizar la rotación del sólido rígido respecto a su eje de giro. ¿Cómo procederemos? Podemos imaginar un disco plano, en lugar de una masa puntual, y calcular el momento angular L_i  de cada partícula respecto a dicho eje de rotación . La suma de cada uno de ellos es, justamente, el momento angular del disco. Empecemos.

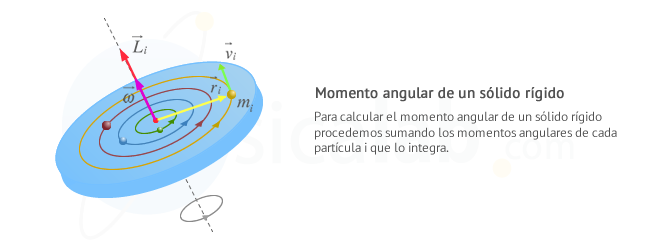
El momento angular de cada partícula genérica i viene dado por:

$${\overrightarrow{L}}_i={\overrightarrow{r}}_i\times {\overrightarrow{p}}_i$$

Teniendo en cuenta que en los movimientos circulares ambos vectores son perpendiculares, podemos desarrollar la expresión del módulo del momento angular de cada partícula tal y como vimos antes:

$$\begin{gathered} L_i=r_i·p_i·\sin \left(90\right)=r_i·p_i=r_i·m_i·v_i\underset{\left[1\right]}{=}{r}_i·m_i·\left({\omega }_i·r_i\right)=m_i·{r_i}^2·{\omega }_i \\ \left[1\right]v_i={\omega }_i·r_i \end{gathered}$$

Ahora bien, la velocidad angular de cada partícula ${\omega }_i$  es la misma, la llamaremos $\omega$ , por lo que podemos escribir:

$$\begin{gathered} L_{\mathrm{total}}=L_1+L_2+\dots +L_n=m_1·{r_1}^2·\omega +m_2·{r_2}^2·\omega +\dots +m_n·{r_n}^2·\omega \Rightarrow \\ \Rightarrow L_{\mathrm{total}}=\left(m_1·{r_1}^2+m_2·{r_2}^2+\dots +m_n·{r_n}^2\right)·\omega \Rightarrow \\ \Rightarrow L_{\mathrm{total}}=\left(\sum _{i=1}^n{m}_i·{r_i}^2\right)·\omega \end{gathered}$$

Como $\overrightarrow{\omega }$  puede considerarse una magnitud vectorial perpendicular al plano de giro y con el sentido que determine la regla de la mano derecha, podemos escribir:

$${\overrightarrow{L}}_{\mathrm{total}}=\left(\sum _{i=n}^n{m}_i·{r_i}^2\right)·\overrightarrow{\omega }$$ 

Observa que, el término entre paréntesis se asemeja a la expresión del momento de inercia de una partícula. Decimos que $I=\sum _{i=1}^n{m}_i·{r_i}^2$  es el momento de inercia del sólido rígido discreto. A partir de él, podemos definir el momento angular del sólido rígido.

Para llegar a la expresión anterior del momento angular hemos considerado como referencia el eje de giro de un disco. En general, la elección de un eje adecuado tiene importancia para el cálculo del momento angular.

Observa que, tal y como venimos diciendo, las expresiones $\overrightarrow{L}=I·\overrightarrow{\omega }$  y $\overrightarrow{p}=m·\overrightarrow{v}$  presentan analogías:

• En el momento angular la velocidad angular $\overrightarrow{\omega }$  está presente. En el momento lineal la velocidad lineal $\overrightarrow{v}$  está presente
• En el momento angular el momento inercial I se opone a los cambios en el estado de rotación del cuerpo. En el momento lineal la masa m se opone a los cambios en el estado de traslación

Finalmente, sabemos que para variar el momento lineal hemos de ejercer una fuerza. ¿Adivinarías qué hemos de hacer para variar el momento angular?

Variación del momento angular en el tiempo

Para saber qué hemos de hacer para variar el momento angular de un cuerpo, vamos a derivar su momento angular respecto al tiempo.

$$\frac{d\overrightarrow{L}}{dt}=\frac{d\left(\overrightarrow{r}\times \overrightarrow{p}\right)}{dt}\underset{\left[1\right]}{=}\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{p}+\overrightarrow{r}\times \frac{d\overrightarrow{p}}{dt}$$ 

Donde en [1] hemos aplicado la definición de derivada de un producto como $\left(a\times b\right)\text{'}=a\text{'}\times b+a\times b\text{'}$ .

Ahora, $\frac{d\overrightarrow{r}}{dt}=\overrightarrow{v}$  y $\overrightarrow{v}$  y $\overrightarrow{p}$  son paralelos por lo que su producto vectorial es nulo, es decir, $\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{p}=0$ . Por otro lado $\frac{d\overrightarrow{p}}{dt}=\overrightarrow{F}$  quedando finalmente:

$$\frac{d\overrightarrow{L}}{dt}=\overrightarrow{r}\times \overrightarrow{F}=\overrightarrow{M}$$

Observa que cuando hablamos de momento de fuerza nos referimos al momento del vector fuerza respecto al origen o eje considerado. La expresión anterior es válida para partículas puntuales, pero también lo es para sistemas de partículas, en los que sólo el momento de las fuerzas externas al propio sistema puede producir cambios en el momento angular del sistema.

Conservación del momento angular

A partir de la expresión anterior, podemos determinar cuándo se conserva el momento angular, según estemos en una partícula puntual o en un sólido rígido.

Observa que existen fundamentalmente dos condiciones bajo las cuales se cumple lo anteior

1. La fuerza neta $\overrightarrow{F}$  que actúa sobre la partícula es nula
2. La fuerza $\overrightarrow{F}$  es paralela a $\overrightarrow{r}$ . Esto se cumple en el caso de las fuerzas centrales

Ejemplos

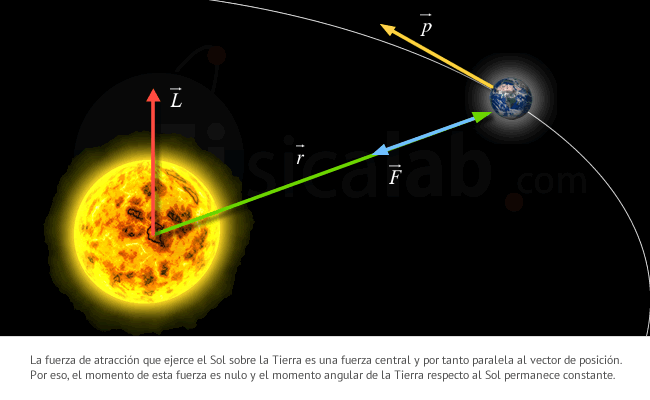
Los sistemas planetarios son sistemas de fuerzas centrales. La Tierra experimenta fuerzas atractivas definidas por la ley de la Gravedad y dirigidas hacia el centro de Sol. Su momento angular es constante.

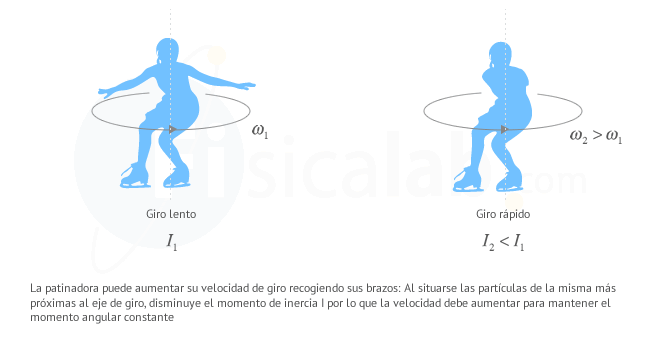
Una patinadora que mientras gira  recoge sus brazos es otro ejemplo interesante. Al recoger sus brazos la distribución de masas respecto al eje varía: toda la masa se concentra más cerca del mismo por lo que el momento de inercia disminuye. En el movimiento de plegar los brazos no son necesarios momentos de fuerza, por lo que el momento angular permanece constante. Observa qué ocurre entonces:

$${\left(I_1·{\omega }_1\right)}_{\text{antes}}={\left(I_2·{\omega }_2\right)}_{\text{después}}$$ 

Esto significa que, dado que I₂ es menor que I₁, la velocidad angular ${\omega }_2$  debe ser mayor que ${\omega }_1$ . Es decir, cuando el patinador pliega sus brazos, su velocidad angular aumenta.