Rotación del Sólido Rígido
Un sólido rígido realiza un movimiento de rotación cuando sus partículas describen circunferencias alrededor de una recta llamada eje de rotación. Para caracterizar el estado de rotación de un cuerpo recurrimos en Física a su momento angular. Sabemos que para cambiar el momento angular, es decir, el estado de rotación del cuerpo, es necesario que actúe una fuerza que genere un momento respecto a un punto o eje de rotación.
En este apartado vamos a estudiar con cierto detalle dicho momento de fuerza. Además presentaremos un nuevo concepto: el par de fuerzas, que nos permitirá producir en los cuerpos un movimiento de rotación pura (esto es, sin traslación). Finalmente estudiaremos la energía cinética de rotación de los cuerpos.
Momento de una fuerza
Imagínate por un momento abriendo o cerrando una pesada puerta. Observa que:
- Instintivamente tratarás de ejercer la fuerza a la mayor distancia posible del eje de giro. Así pues, la asociación fuerza-distancia es responsable de la rotación de la puerta.
- De igual manera tratarás que la dirección de la fuerza que apliques será perpendicular a la puerta.
Para caracterizar la capacidad de una fuerza para producir la rotación de un cuerpo, a partir de estas dos ideas, introducimos el concepto de momento de fuerza.
El momento de fuerza, también conocido como momento dinámico, torque o, simplemente, momento es el momento del vector fuerza,
- Respecto al punto O:
- Respecto al eje e:
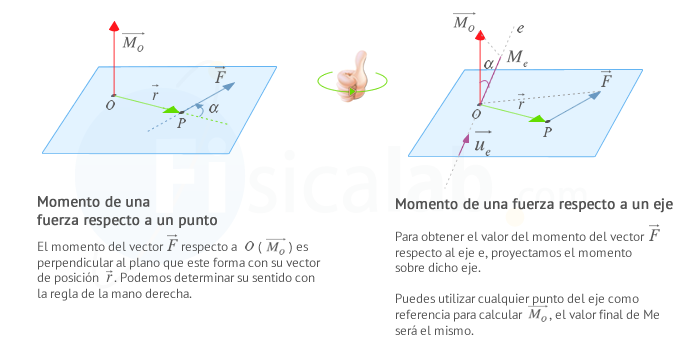
Observa que en dinámica podemos decir que:
- Las fuerzas son responsables de modificar la traslación de los cuerpos, es decir, son el agente dinámico de traslación
- El momento de fuerza es responsable de modificar la rotación de los cuerpos, es decir, el agente dinámico de rotación
El momento de una fuerza nos permite conocer la capacidad de dicha fuerza para cambiar el estado de rotación del cuerpo alrededor de un eje de rotación que pase por dicho punto. Para cambiar dicho estado el momento, o alguna de sus componentes, debe actuar en la dirección del eje de rotación.
Volvamos ahora a nuestro ejemplo de la puerta y asociemos lo que hemos aprendido hasta ahora.
- Cuanto mayor sea
- En relación a la dirección de la fuerza, cuanto más perpendicular al eje de giro sea la fuerza, máyor es la componente del momento en dicho eje y por tanto más facilidad en abrir o cerrar la puerta. Llevando este razonamiento al extremo, a nadie se le ocurre abrir o cerrar una puerta empujando el pomo hacia arriba o hacia abajo. En tal caso, la dirección de la fuerza es paralela al eje y por tanto el momento de dicha fuerza es perpendicular al mismo, es decir, no hay componentes del momento que actúen en la dirección del eje de rotación y por tanto el giro es imposible

Una vez hemos presentado el agente de rotación en dinámica, el momento de fuerza, vamos a estudiar cuándo se produce un movimiento de rotación pura.
Par de fuerzas
Repasemos por un momento lo que hemos aprendido hasta ahora:
- Para saber como se traslada el sólido rígido estudiamos su centro de masas, aplicando al mismo la resultante de todas las fuerzas externas que actúan sobre el cuerpo, tal y como vimos al estudiar el compotamiento dinámico del centro de masas
- Para caracterizar el estado de rotación de un cuerpo, estudiamos su momento angular
- Si queremos modificar el estado de rotación de un cuerpo, esto es, su momento angular, debemos aplicar una fuerza que genere un momento
Observa que, según se deduce del primer punto, si aplicamos una fuerza a un sólido rígido este se trasladará. ¿Cómo podemos entonces generar un movimiento de rotación pura? Para ello vamos a introducir un nuevo concepto: el par de fuerzas.
Un par de fuerzas es un sistema de dos fuerzas paralelas de igual valor (módulo) pero sentido contrario. Actúan sobre el mismo cuerpo pero sobre líneas de acción diferentes.
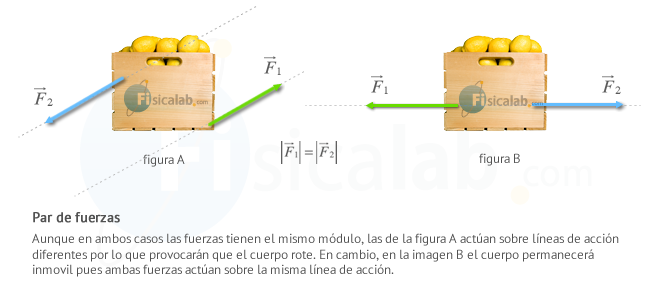
Si sobre un sólido rígido actúa un par de fuerzas, aparece un movimiento de rotación pura.
Ahora observa. Hemos dicho que para producir una rotación pura necesitamos un par de fuerzas. Puede que te estés preguntando, entonces, cómo es posible que se produzca una rotación pura en la puerta del apartado anterior, cuando sólo aplicamos una fuerza sobre la misma. La razón es simple: el eje de giro posibilita la aparición de una fuerza de reacción de igual dirección y sentido contrarior a la aplicada, apareciendo el par necesario para la rotación del sólido.
En la siguiente imagen puedes observar distintos ejemplos en los que se produce la rotación a partir de una fuerza y un eje de giro, que posibilita que aparezca la fuerza de reacción.

Finalmente, vamos a justificar que, efectivamente, el par de fuerzas no genera un movimiento de traslación a partir de la ecuación fundamental de la dinámica de traslación de un sistema de partículas. Ten presente, una vez más, que el efecto que provocan varias fuerzas exteriores en el movimiento de traslación de un sólido rígido se determina aplicando la resultante
Es decir, el centro de masas no modifica su estado de movimiento debido al par de fuerzas: permanece en reposo o con movimiento rectilíneo uniforme.
Una vez queda claro que necesitamos un par de fuerzas para producir una rotación pura, vamos caracterizarlo cuantitativamente. Para ello vamos a introducir el momento de un par de fuerza.
Momento de un par de fuerzas
Para caracterizar un par de fuerzas determinado, recurrimos a su momento. Recuerda que las dos fuerzas del par tienen igual módulo.
El momento de un par de fuerzas viene dado por:
Donde:
Observa que se trata de una magnitud vectorial propia del par de fuerzas, es decir, independiente del origen de coordenadas elegido como referencia.
-
Su módulo es el producto del módulo de cualquiera de las fuerzas por el brazo del par, es decir, la distancia d entra las lineas de acción de las dos fuerzas
- Su dirección es perpendicular al plano definido por el par de fuerzas
- Su sentido se obtiene con la regla de la mano derecha
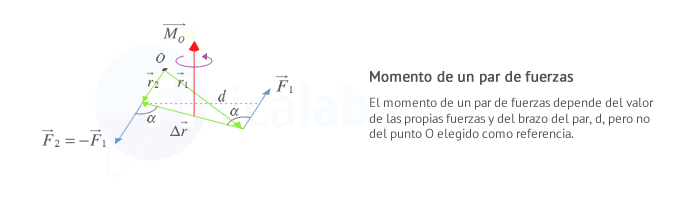
Comprobación
Efectivamente, para comprobar la expresión del momento del par de fuerzas elegimos un origen de coordenadas arbitrario, calculamos el momento de cada fuerza respecto a el y los sumamos.
Energía cinética de rotación
Los cuerpos, cuando se mueven, tienen la capacidad de transformar su entorno. Por ejemplo, si lanzas una bola contra un grupo de bolos que se encuentran en reposo, estos saldrán despedidos cuando impacte contra ellos. A esta capacidad producir transformaciones es a lo que llamamos en física energía.
La energía cinética de los cuerpos es la capacidad que tienen de producir transformaciones por el hecho de encontrarse en movimiento. Hasta ahora habíamos estudiado exclusivamente la energía cinética de traslación de los cuerpos. El punto material solo es capaz de trasladarse, pero no de rotar, pues carece de extensión. El sólido rígido, en cambio, puede rotar, y por tanto a la energía cinética de traslación del cuerpo habrá que sumar la contribución de la rotación.
La energía cinética del sólido rígido tiene dos contribuciones, la asociada al movimiento de traslación y la asociada al movimiento de rotación. En el caso de que el eje de rotación interno del cuerpo pase por el centro su masas, podemos aplicar la siguiente expresión:
Donde:
- m: Masa del cuerpo en movimiento. Representa una oposición al cambio en el estado de traslación del cuerpo. A mayor masa, mayor dificultad de cambiar la velocidad del cuerpo. Su unidad de medida en el Sistema Internacional (S.I.) es el kilogramo ( kg )
- I : Momento de inercia del sólido. Representa un factor de oposición a los cambios en el estado de rotación del cuerpo. Depende de la masa del sólido y de la distribución de dicha masa con respecto al eje de rotación elegido. Aunque en general existen infinitos momentos de inercia posibles, tanto como ejes de rotación se puedan elegir, su expresión, para el caso del sólido rígido discreto, es:
Observa el paralelismo que hay entre los factores asociados a la traslación y a la rotación.
- m - I: La oposición al cambio traslacional - rotacional respectivamente
Observa, así mismo, que al igual que podíamos relacionar la energía cinética de traslación con el módulo del momento lineal según la expresión
Comprobación
La expresión de la energía cinética de traslación es simplemente el valor de la energía cinética 1/2·m·v2 aplicada al centro de masas del cuerpo.
Para deducir la expresión de la energía cinética de rotación de todo el sólido rígido, de n partículas, calculamos la energía cinética de cada partícula i respecto al centro de masas y sumamos sus contribuciones individuales:
Donde hay que tener en cuenta que la velocidad angular de todas las partículas del sólido es la misma.
Cuerpos rodantes
En la naturaleza abundan ejemplos del movimiento de rotación de los cuerpos. En la mayoría de los casos la rotación se produce en combinación con la traslación. En tal caso decimos que pueden ser:
- Independientes. No hay relación entre la rotación y la traslación del cuerpo. Por ejemplo la Tierra en su recorrido alrededor del Sol
- Acoplados: La velocidad de traslación y rotación se encuentran relacionadas. Por ejemplo un cilindro rodando en un plano inclinado
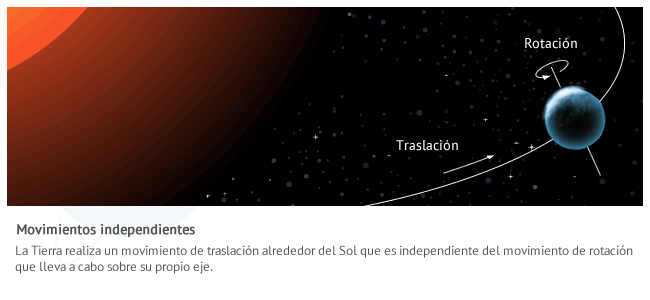
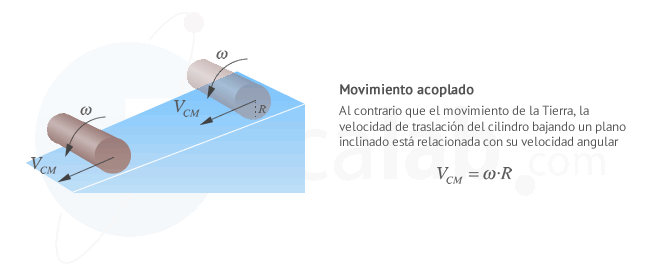
El caso del cilindro rodante es muy ilustrativo de un hecho que, a primera vista, puede resultar paradójico: un cuerpo que se deja resbalar desde una determinada altura llega antes que otro que se deja rodar desde esa misma altura. La razón es que en el primer caso toda la energía potencial gravitatoria se transforma en energía cinética de traslación al llegar a la base del plano mientras que, en el segundo caso, parte de la energía potencial se transforma en energía cinética de rotación. Visto desde un punto de vista cinemático, la velocidad en cualquier punto siempre será menor en el caso de que el cuerpo haya llegado a ese punto deslizandose:
- Conversión de energía en cuerpo deslizante:
- Conversión de energía en cuerpo rodante:
Finalmente observa que, aunque hemos considerado que no existe rozamiento entre el cuerpo y la superficie del plano inclinado, en el caso del cuerpo rodante es necesario un rozamiento mínimo que permita la rotación. Desde el punto de vista energético dicho rozamiento será despreciable y las expresiones anteriores son perfectamente válidas.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
