La cinemática es la parte de la física que se encarga del estudio del movimiento, sin importarle las causas que lo producen. En este cuestionario de autoevaluación te invitamos a que profundices sobre los conocimientos adquiridos en el tema de cinemática bidimensional.
La cinemática es la parte de la física que se encarga del estudio del movimiento, sin importarle las causas que lo producen. En este cuestionario de autoevaluación te invitamos a que profundices sobre los conocimientos adquiridos en el tema de cinemática bidimensional.
Antes de comenzar, te recomendamos que repases los conceptos más importantes de dicho tema ¡No hagas trampa!
Si tienes los conceptos bien afianzados, resolver el cuestionario no debería llevarte más de 15 minutos.
- Tu puntuación:
- Puntuación de paso:
Revisa las respuestas correctas con sus soluciones en las pestañas de cada pregunta, y ¡no te olvides de compartir con tus amigos!
(1 puntos)
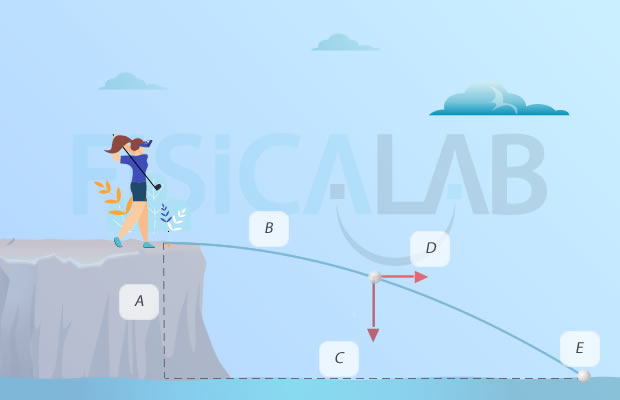
Identifica las variables en el tiro horizontal de la siguiente imagen.
- A: Altura inicial
- B: Trayectoria
- C: Alcance
- D: Descomposición cartesiana del vector velocidad
- E: Proyectil
- A y C: Distancia
- B: Trayectoria
- D: Descomposición cartesiana del vector aceleración
- E: Proyectil
- A: Altura inicial
- B: Celeridad
- C: Nivel del mar
- D: Descomposición cartesiana del vector aceleración
- E: Bala
- A: Altura inicial
- B: Trayectoria
- C: Alcance
- D: Descomposición cartesiana del vector velocidad
- E: Proyectil
(1 puntos)
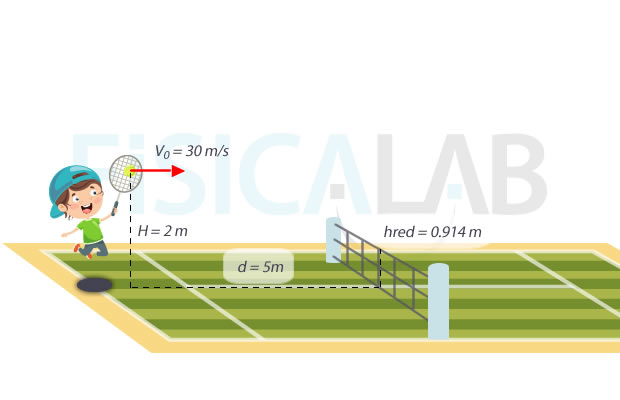
¿Pasará la pelota la red?
Sí, la pelota pasa a 0.946 m de la red.
Sí, la pelota pasa a 0.522 m de la red.
No, a la pelota le faltan 0.123 m para poder pasar la red.
No, a la pelota le faltan 0.242 para poder pasar la red.
Para calcular la altura a la que pasa la pelota sobre la red, en primer lugar deberemos saber en que instante de tiempo pasa por encima de ella. Para ello, sabiendo que la pelota se encuentra a 5 m y que avanza con un m.r.u. a 30m/s:
En ese instante de tiempo la pelota se encuentra justo sobre la red, basta con calcular la coordenada y de su posición y casi habremos resuelto el problema:
Teniendo en cuenta que la red tiene una altura de 0.914 m, pasará a una distancia de 1.86-0.914 = 0.946 m de la misma.
(1 puntos)
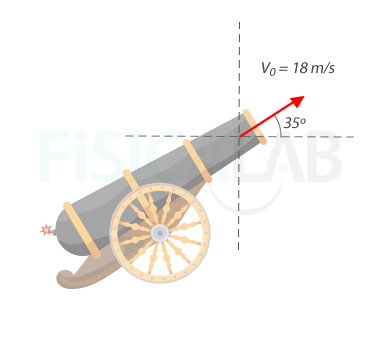
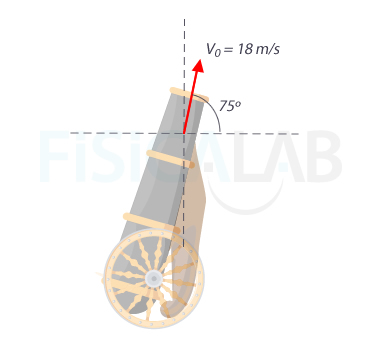
Suponiendo que no existe resistencia del aire, y sin realizar ningún cálculo ¿en cuál de estas configuraciones el proyectil va a llegar más lejos respecto a la vertical del cañón?
El alcance es el mismo.
Como puedes comprobar tú mismo utilizando el siguiente Experimenta y aprende, el ángulo máximo para una algura inicial 0 se obtiene a los 45º. Como 75º se aleja 30º de 45º, más que 35º, es 35º el ángulo que obtiene mayor alcance.
(1 puntos)
Suponiendo que no existe resistencia del aire, y sin realizar ningún cálculo ¿cuál de estos proyectiles crees que conseguirá un alcance mayor?
Los dos tendrán el mismo alcance.
Puesto que no hay rozamiento, la masa no influye (tampoco la forma del objeto), con lo que ambos cuerpos llegarán al mismo punto (tendrán el mismo alcance).
(1 puntos)
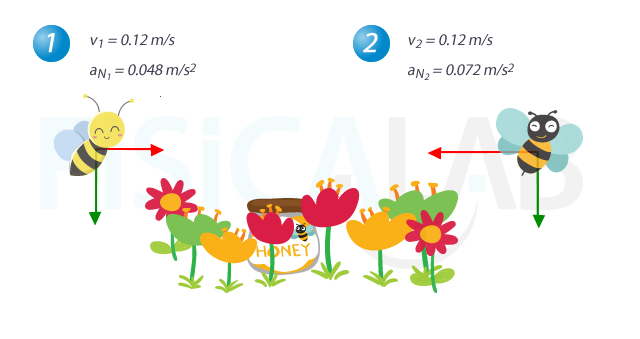
Sabiendo que las dos abejas de la figura se encuentran describieindo un movimiento circular uniforme, ¿cuál de ellas tiene un radio de giro mayor?
La primera, con un radio de giro de 30 cm.
La segunda, con un radio de giro de 20 cm.
La primera, con un radio de giro de 40 cm.
La segunda, con un radio de giro de 30 cm.
Tenemos el valor de la velocidad y de la aceleración normal, y estas se encuentran relacionadas según la expresión:
Si despejamos R, podemos tener el valor del radio de giro de cada movimiento:
Por tanto, el radio de giro del cuerpo 1 es mayor.