Magnitudes Angulares
Las magnitudes angulares, como su propio nombre indica, están referidas a ángulos. Entre otras cosas nos permiten estudiar los movimientos circulares. En este apartado vamos a presentarte las principales. Veremos:
- Las unidades para medir ángulos: radianes y grados
- La posición angular
- El desplazamiento referido a un ángulo: desplazamiento angular
- Qué es la velocidad angular
- La expresión de la aceleración angular
- Un repaso de la aceleración normal
- La relación que guardan las magnitudes angulares y la lineales
- Una breve introducción a las magnitudes angulares como vectores
Radianes y Grados
La unidad en el Sistema Internacional (S.I.) para medir ángulos es el radián (rad). Una circunferencia tiene 2π radianes. Por otro lado, podemos medir los ángulos en grados. Una circunferencia tiene 360º. Teniendo en cuenta la relación anterior, para convertir entre grados y radianes puedes utilizar la siguiente expresión:
Posición Angular
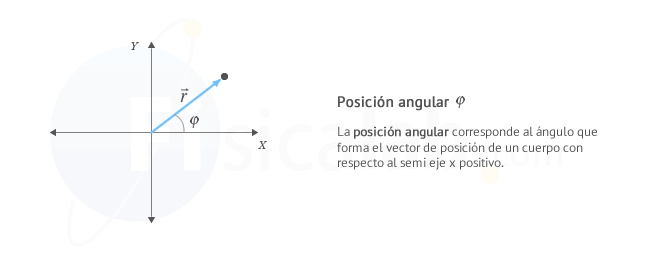
La posición angular φ es una magnitud angular fundamental que representa el ángulo que forma en cada momento el vector de posición de un cuerpo con el semieje X positivo. Su unidad en el Sistema Internacional de Unidades (S.I.) es el radián (rad).
Desplazamiento Angular
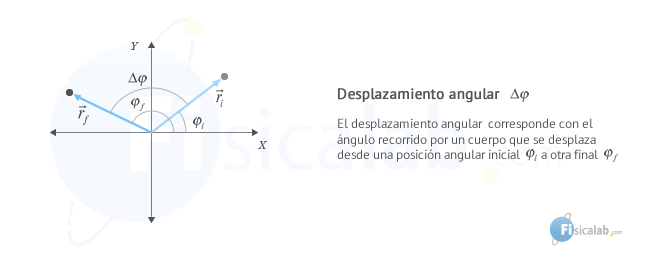
El desplazamiento angular (∆φ) representa el ángulo recorrido. Viene dado por la diferencia entre una posición angular final φf y una posición angular inicial φi:
Velocidad Angular
Representa el desplazamiento angular (∆φ) experimentado por un cuerpo en cada segundo. Su unidad en el Sistema Internacional de Unidades (S.I.) es el rad/s aunque en ocasiones verás que se puede utilizar también las revoluciones o vueltas por minuto, r.p.m. (1 r.p.m. = 2π/60 rad/s). Al igual que sucedía con la velocidad, existe la velocidad angular media ωm y la velocidad angular instantánea ω (o simplemente velocidad angular) según se considere un intervalo de tiempo ∆t o un instante de tiempo respectivamente dt.
| ωm | ω |
|---|---|
Aceleración Angular
Representa la variación de velocidad angular (∆ω) respecto del tiempo. Su unidad en el Sistema Internacional de Unidades (S.I.) es el rad/s2. Al igual que sucedía con las magnitudes lineales equivalentes, existe la aceleración angular media αm y la aceleración angular instantánea α (o simplemente aceleración angular) según se considere un intervalo de tiempo ∆t o un instante de tiempo respectivamente dt.
| αm | α |
|---|---|
Aceleración Normal o Centrípeta
Aunque no es una magnitud angular, propiamente dicha, pues no se mide en unidades angulares, es importante recordar aquí la expresión de la aceleración normal o centrípeta.
Recuerda que la aceleración normal o centrípeta es la responsable del cambio de dirección del vector velocidad y es por ello que aparece en todos los movimientos circulares.
Relación entre Magnitudes Angulares y Lineales
Podemos relacionar las magnitudes angulares y lineales en los movimientos circulares a través del radio R.
| Magnitud Lineal | Relación | Magnitud Angular |
|---|---|---|
| s | φ | |
| v | ω | |
| at | α | |
| an | - |
Vectores de Magnitudes Angulares
Hasta ahora hemos estudiado las magnitudes angulares como magnitudes escalares. En realidad, se trata de magnitudes vectoriales pero para los propósitos de este nivel, las consideraremos escalares. No obstante, adelantamos aquí la relación que guardan la velocidad lineal con la angular y la aceleración tangencial con la angular, en forma vectorial, que viene dada a través del producto vectorial:
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
