Centro de masas de 4 partículas en un plano
Enunciado
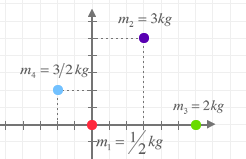
Encuentra el centro de masas de las partículas que aparecen en la figura. Se supone que el sistema es rígido y el sistema de referencia se encuentra expresado en metros.
Solución
Datos
- m1 = 1/2 kg
- m2 = 3 kg
- m3 = 2 kg
- m4 = 3/2 kg
Consideraciones previas
- Se nos indica que las distancias entre las partículas son rígidas. Es por tanto un sólido rígido y tiene sentido que nos preguntemos por el centro de masas.
- Todas las partículas se encuentran en un plano, por lo que podemos despreciar la coordenada z (z = 0 en todas)
Resolución
La posición del centro de masas viene dada por:
Por tanto, aplicando a nuestras 4 partículas, separando las coordenadas x e y nos queda:
Es decir, el vector de posición del centro de masas es:
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
