Momento de inercia respecto a distintos ejes
Enunciado
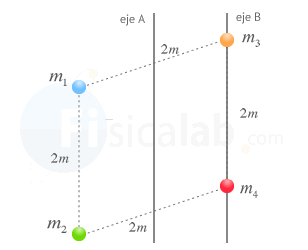
Determina el momento de inercia del sistema de partículas de la figura respecto a cada uno de los ejes representados teniendo en cuenta que m1 = 4 kg ; m2 = 2 kg ; m3 = 3 kg y m4 = 2 kg.
Solución
Datos
- m1 = 4 kg ; m2 = 2 kg ; m3 = 3 kg ; m4 = 2 kg
- Lado del cuadrado en el que se disponen las partículas l = 2 m
Resolución
El momento de inercia viene dado por la expresión
Como puede observarse, el momento de inercia depende de como se distribuyan las masas respecto al eje elegido.
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
