Campo magnético en el centro de cuatro corrientes rectilíneas
Enunciado
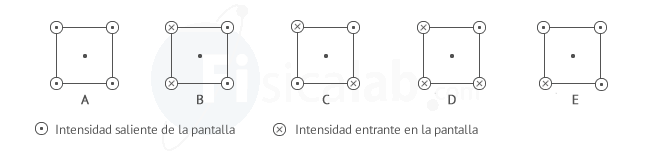
Cuatro conductores rectilíneos situados en los vértices de un cuadrado generan un campo magnético dependiendo del valor y sentido de cada una de sus intensidades de corriente. Suponiendo que todas las intensidades I son la misma, dibuja el campo magnético generado en cada uno de los siguientes supuestos:
Solución
Caso a)
Según el prinicipio de superposición del campo magnético, el campo magnético creado en cualquier punto será la suma de los campos magnéticos generados individualmente por los distintos elementos que se encuentren "próximos" a dicho punto. En nuestro caso, el campo magnético en el centro del cuadrado será la suma de los campos magnéticos creados por cada una de las corrientes rectilíneas.
Si sitúas el pulgar de tu mano derecha orientada saliendo de tu pantalla cuando la corriente es saliente o entrando cuando la intensidad es entrante (regla de la mano derecha) el resto de dedos de tu mano describirán la forma y sentido de las líneas de campo magnetico. Dichas líneas se caracterizan porque el vector intensidad del campo magnético es tangente en cada uno de sus puntos. Si dibujamos como serían, dichas líneas y sus respectivos vectores en el punto centro obtenemos que:
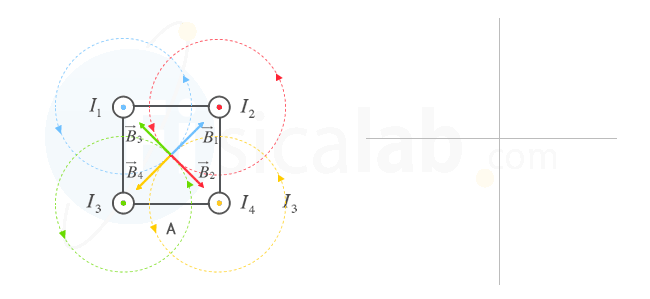
Dado que el valor de la intensidad es la misma, el módulo de todos los vectores es también el mismo. Esta disposición de las corrientes provoca que existan cuatro vectores con el mismo módulo aunque orientados de forma contraria por lo que el vector campo magnético resultante será 0, es decir, finalmente no habrá vector. B4 se anula con B1 y B3 con B2.
Caso b)
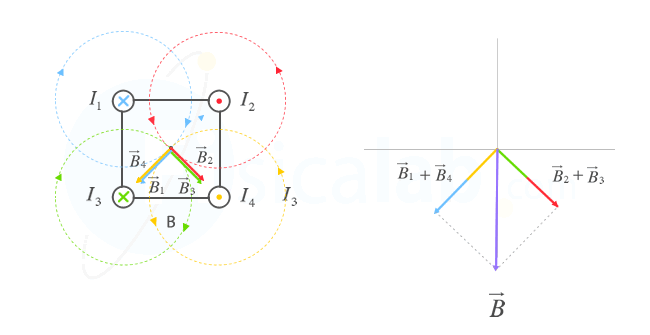
En este caso B2-B3 y B1-B4 tienen la misma dirección y sentido. Si aplicamos el concepto estudiado en la suma vectorial, obtenemos que el campo magnético total apunta hacia abajo.
Caso c)

Caso d)

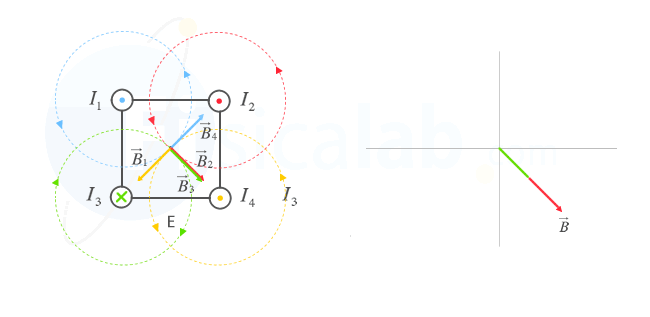
Caso e)
No hemos encontrado ninguna fórmula destacable en este ejercicio.
