Ley de Lorentz
En apartados anteriores hemos estudiado como las cargas en movimiento, ya sea de forma individual o en conjunto (corrientes eléctricas) son capaces de crear un campo magnético.
En esta ocasión estudiaremos el caso contrario; ¿Qué les ocurren a las cargas eléctricas cuando se introducen en el seno de un campo magnético? Vamos a ello.
Fuerza de Lorentz
Al contrario que en los campos eléctricos, una partícula cargada que se encuente en reposo en el interior de un campo magnético no sufre la acción de ninguna fuerza. Otra caso bien distinto se produce cuando la partícula se encuentre en movimiento, ya que por el contrario, en este caso, la partícula si que experimentará la acción de una fuerza magnética que recibe el nombre de fuerza de Lorentz.

Por tanto, los campos magnéticos son generados por cargas en movimiento y sólo ejercen una acción sobre cargas eléctricas que se encuentran en movimiento.
La ley de Lorentz establece que una partícula cargada q que circula a una velocidad
De la ecuación anterior podemos extraer las siguientes conclusiones:
- Su módulo es
- Su dirección es perpendicular al plano que forman
- Su sentido será el de
De una forma gráfica es posible determinar la dirección y sentido de la fuerza de Lorentz aplicando la regla de la mano derecha. Para ello sitúa tu mano derecha de tal forma que tu dedo índice coincida con la dirección y sentido del vector velocidad, el medio (o corazón) coincida con la dirección y sentido del campo magnético. Si la carga es positiva, tu dedo pulgar estará indicando la dirección y sentido de dicha fuerza. Si es negativa estará indicando su dirección aunque el sentido será el contrario del que marca tu pulgar.
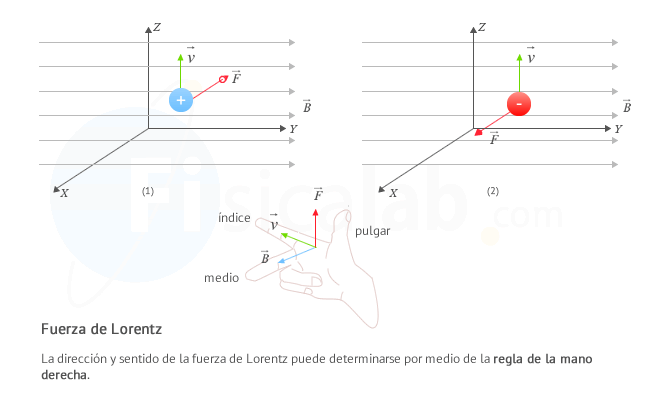
En resumen, según la expresión de la ley de Lorentz la fuerza de Lorentz será:
- Nula
- Si la partícula no posee carga. q = 0 -> F = 0.
- Si la partícula está en reposo. v = 0 -> F = 0.
- Si la velocidad de la partícula es paralela al campo. F = |q|·v·B·sen 0 -> F = 0
- Máxima. Si v y B son perpendiculares ( α = 90º ) entonces F = |q|·v·B·sin 90 = |q|·v·B.
El trabajo y la aceleración en la Fuerza de Lorentz
Imagina la trayectoría de una partícula cargada que se encuentra en el interior de un campo magnético. Por definición, el vector velocidad de cualquier partícula es siempre tangente a la trayectoria que describe. Adicionalmente sabemos que la fuerza de Lorentz es siempre perpendicular a v, por tanto independientemente de que el campo magnético sea uniforme o no, la fuerza de Lorentz es siempre normal a la trayectoria.
De este razonamiento podemos extraer que si únicamente actúa la fuerza de Lorentz:
- La partícula no posee aceleración tangencial, únicamente aceleración normal. Esto implica que el módulo del vector velocidad no cambia (no se ve alterada la celeridad o rapidez de la partícula) pero si lo puede hacer su dirección.
- Dado que la fuerza es perpendicular al desplazamiento que se produce en la trayectoria, el trabajo de la fuerza de Lorentz es nulo. Por tanto, en los campos magnéticos la energía cinética de una partícula permanece constante.
Una partícula cargada que se encuentra en el interior de un campo magnético sufre una fuerza magnética (fuerza de Lorentz) normal a la trayectoria que le provoca cambios en la dirección de su vector velocidad aunque no en su módulo, provocando que su energía cinética permanezca constante.
¿Qué es un Tesla?. Definición.
La relación que establece la ley de Lorentz es utilizada para definir la unidad de intensidad de los campos magnéticos en el Sistema Internacional S.I.. Como ya habrás podido comprobar en apartados anteriores dicha unidad recibe el nombre de Tesla, en honor al físico yugoslavo Nikola Tesla (1856-1943). Y aunque la hemos utilizado con anterioridad, no podíamos definirla hasta conocer esta ley.
Un tesla es la intensidad de un campo magnético que provoca una fuerza de un newton a una partícula cargada de un culombio que se mueve a una velocidad de un metro por segundo perpendicularmente a dicho campo magnético.
Para que te hagas una idea, el campo magnético terrestre a nivel del mar oscila entre los 3·10-5 y 5·10-5 T. Una barra de imán normal puede oscilar entre los 0.2 o 0.3 T y los campos magnéticos más intensos jamás obtenidos pueden alcanzar a lo sumo los 1000 T. Como puedes comprobar, el tesla se trata de unidad extremadamente grande para la mayor parte de los campos magnéticos, por lo que suele utilizarse una unidad menor denominada gauss (G). El tesla y el gauss se relacionan de la siguiente manera:
Movimiento de una partícula cargada en un campo magnético uniforme
En los campos magnéticos uniformes, las partículas cargadas en movimiento describen trayectorias muy características que merecen ser estudiadas. En concreto podemos encontrar dos tipos de movimientos, el que se produce cuando el vector velocidad de la partícula es o no es perpendicular a las líneas de campo magnético uniforme que atraviesa.
Velocidad perpendicular a las líneas de campo
Tal y como hemos comentado anteriormente, cuando
Dado que la única aceleración existente es la normal y además es constante, la partícula cargada describirá un movimiento circular uniforme.
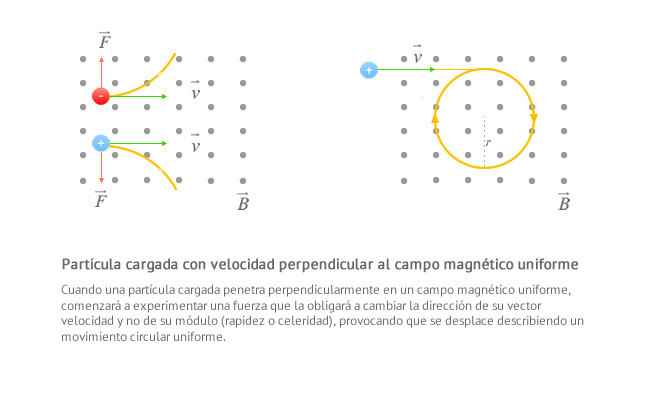
Una partícula cargada que atraviesa una campo magnético uniforme en dirección perpendicular a dicho campo describe un movimiento circular uniforme cuyo sentido dependerá del signo de la partícula cargada.
A partir de la expresión de la aceleración normal calculada anteriormente, podemos obtener el resto de magnitudes características de los m.c.u.:
Radio
Esta expresión tiene una importancia especial, ya que por de manifiesto que a mayor carga de las partículas, menor será el radio del m.c.u. Esto es el fundamento de determinados dispositivos que estudiaremos a continuación como por ejemplo el espectrómetro de masas.
Velocidad Angular
Período
Velocidad no perpendicular a las líneas de campo
Cuando una partícula intenta atravesar oblícuamente un campo magnético uniforme, es decir, su velocidad no es perpendicular a las líneas de campo, esta se puede descomponer en dos componentes vx y vy. La primera de ellas en la dirección del campo y la segunda perpendicular al campo. Esto provocará que al ser vx paralela al campo se mantendrá constante su velocidad en esa dirección ya que la fuerza en esa componente será nula. Sin embargo, debido a vy si que aparecerá una fuerza que provocará un movimiento circular uniforme en la dirección perpendicular al campo. En resumen, tendremos dos tipos de movimiento:
- Un movimiento rectilíneo uniforme en la dirección del campo.
- Un movimiento circular uniforme en la dirección paralela al campo.
Una partícula cargada que se introduce oblicuamente en un campo magnético uniforme comienza a describir un movimiento helicoidal como resultado de la composición de un movimiento rectilíneo uniforme y un movimiento circular uniforme.
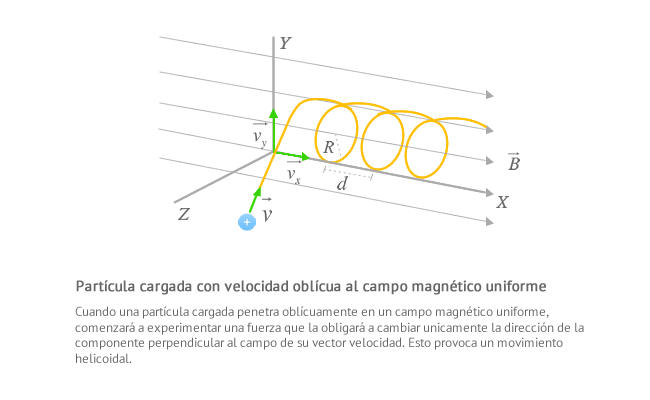
Algunas de las magnitudes propias de este movimiento helicoidal son las siguientes:
Radio
Paso de hélice
Periodo
Fuerza de Lorentz Generalizada
Los campos eléctricos y magnéticos están tan relacionados que es normal que una partícula cargada entre en una región del espacio en el que convivan al mismo tiempo ambos tipos de campo. Esto implicará que dicha partícula se encuentra sometida a dos fuerzas:
1. Una fuerza en la dirección del campo eléctrico.
2. Una fuerza perpendicular al campo magnético.
Si tenemos en cuenta el principio de superposición de fuerzas, la fuerza total que actúa sobre una partícula cargada inmersa simultáneamente en un campo eléctrico y un campo magnético recibe el nombre de fuerza de Lorentz generalizada.
Aplicaciones de la Ley de Lorentz
La aplicación de la ley de Lorentz ha servido para construir distintos tipos de dispositivos que han sido esenciales para comprender la naturaleza de la materia, e incluso para nuestros momentos de ocio. Entre ellos, podemos destacar el selector de velocidades, el espectrómetro de masas o el ciclotrón.
Selector de velocidades
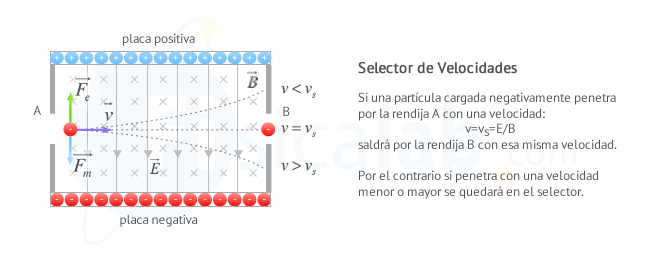
Como su propio nombre indica, el selector de velocidades se trata de un dispositivo basado en la ley de Lorentz que permite la entrada de partículas cargadas dejando pasar unicamante aquellas que posean una determinada velocidad. Principalmente se compone de dos láminas cargadas paralelas (una en frente de la otra) en el que actúan de manera conjunta un campo magnético y un campo eléctrico perpendiculares entre sí. En el comienzo y final de las dos placas se disponen unas rendijas por las que se permite la entrada (A) y salida (B) respectivamente de las partículas.
Cualquier partícula que entre por la rendija A se verá sometida por una fuerza eléctrica y una fuerza magnética con la misma dirección aunque sentidos opuestos, cuyos modulos son:
Para que cualquiera de ellas pueda salir por la rendija B debe seguir una trayectoria recta, lo que implica que la fuerza neta que actúe sobre la partícula debe ser nula, o lo que es lo mismo que Fe=Fm.
Esto implica que fijando unos valores de E y B podemos determinar una cierta velocidad y aquellas partículas que la posean atravesarán en línea recta el dispositivo saliendo por la rendija B, el resto sufrirán desviaciones en el sentido de la fuerza eléctrica o la magnética. Observa que la velocidad es independiente de la masa.
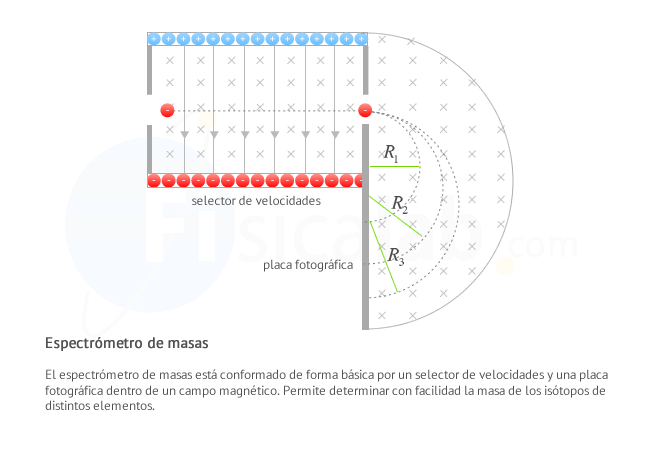
Espectrómetro de masas
Otro dispositivo insteresante para el estudio de la naturaleza de la materia se trata del espectrómetro o espectrógrafo de masas. Se trata de un selector de velocidades por el que se hace pasar isótopos ionizados unidos a una región que posee un campo magnétido perpendicular a la trayectoria de los isótopos. Al salir del selector de velocidades, debido al campo magnético las partículas describen una trayectoria de radio R:
Dado que la carga, velocidad y campo magnético es el mismo para cada una de ellas, el radio de la circunferencia dependerá de la masa de los isótopos. Para determinar el radio se las deja impactar contra una placa fotográfica donde dejará un registro gráfico. Dependiendo de la distancia donde se encuentre el impacto podemos deducir el radio y con este la masa del isótopo que impactó allí.
El ciclotrón
Dado que no podemos preguntar a nadie sobre la composición de las partículas subatómicas, la mejor manera de conocer su composición consiste en hacerlas colisionar para "romperlas" y "ver que contienen". Esta es la misión del ciclotrón, un acelerador de partículas basado en el uso de campos magnéticos que fué inventado en 1932 por el físico norteamericano Ernest O. Lawrence (191-1958). La idea de este dispositivo es la de acelerar protones hasta obtener velocidades muy elevadas con la finalidad de bombardear otros núcleos atómicos y provocar reacciones nucleares que nos proporcionen información sobre la estructura de dichos núcleos.
En la actualidad existen enormes aceleradores de partículas de varios kilometros construidos bajo tierra. En concreto en Europa se encuentran el LEP (Large Electron positron collider) actualmente sustituido por el LHC (Large Hadron Collider) o el SPS (Super Sincrotrón de Protones) del CERN (Conseil Européen por la Recherche Nucléaire) en Suiza, mientras que en Estados Unidos se encuentran otros como el FermiLab (en honor al físico Enrico Fermi) y SLAC (Stanford Linear Accelerator Center).
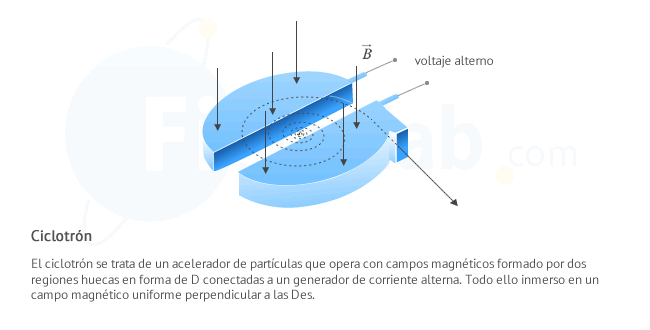
Consta de de dos regiones metálicas huecas con forma de "D" donde se ha practicado el vacío conectadas cada una de ellas a los bornes de un generador de corriente alterna y separadas una cierta distancia, lo que provoca un campo eléctrico en dicha separación. Todo ello se encuentra sometido a la acción de un campo magnético uniforme perpendicular a cada "D" por medio de un electroimán. Al situar en su centro un protón este se verá atraido por la "D" con potencial negativo. Al entrar en ella, debido al campo magnético describirá una semicircunferencia en su interior llegando nuevamente a la separación. Durante ese tiempo el potencial de las "D" a cambiado gracias al generador de corriente alterna y ahora se verá acelerada hacia la otra "D" cuyo potencial ahora es negativo, volviendo a repetir todo el proceso. De esta forma, alternando el potencial eléctrico de las "D" el protón se va acelerando cada vez que cruza la separación aumentando así su velocidad. Una característica importante es que aunque en cada semicircunferencia el protón aumenta la velocidad, también lo hace el espacio que debe recorrer ya que cada vez el radio es más grande, lo que implica que finalmente el tiempo que tarda en recorrer cada semicircunferencia y por tanto el tiempo en el que el generador debe invertir los potenciales es siempre es el mismo:
El radio de la última semicircunferencia coincide con el radio de las "D", por tanto:
Esto implica que el protón saldrá del ciclotrón con una velocidad máxima equivalente a:
y por tanto con una energía cinética máxima cuya expresión es:
Es decir, cuanto mayor sea el radio y el campo magnético del ciclotrón mayor será la velocidad y energía cinética máxima de salida. Sin embargo, a grandes velocidades se producen efectos relativistas, que aumentan la masa de la partícula aumentando el periodo del movimiento, lo que provoca que el cambio de potencial se produzca cuando el protón no está en la separación. Esto puede dar lugar a un proceso de frenado, en vez de aceleración.
Este fué un problema con el que tuvieron que enfrentarse los primeros ciclotrones, hasta que en 1950 surgieron los primeros ciclotrones sincronizados, también conocidos como sincrotrones.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
