Resistencia mixta resultante

Datos

V_A-V_C = 200 V
R₁ = 1 KΩ = 1000 Ω
R₂ = 300 Ω
R₃ = 900 Ω

Resolución

Cuestión a)

Como se puede observar en la figura, disponemos de una asociación mixta ya que por un lado R₁ y R₂ se encuentran en paralelo y ambas en serie con R₃. Vamos a calcular en primer lugar la resistencia equivalente entre R₁ y R₂ y que llamaremos R_1,2.

$$\begin{gathered} \frac{1}{R_{1,2}}=\frac{1}{R_1}+\frac{1}{R_2}\Rightarrow \\ \frac{1}{R_{1,2}}=\frac{1}{1000}+\frac{1}{300}\Rightarrow \\ \underline{R_{1,2}=230.77 \Omega } \end{gathered}$$

Por tanto, podemos sustituir R₁ y R₂ por una resistencia R_1,2 de tal forma que esta última se encuentre en serie con R₃:

A continuación, podemos asociar ambas resistencias en serie y calcular la nueva resistencia equivalente R_1,2,3:

$$\begin{gathered} R_{1,2,3}=R_{1,2}+R_3 \Rightarrow \\ {R}_{1,2,3} = 230.77 + 900 \Rightarrow \\ \boxed{R_{1,2,3}= 1130.77 \Omega } \end{gathered}$$

Cuestión b)

Si tenemos en cuenta la resistencia calculada anteriormente, podemos aplicar la ley de Ohm para calcular el valor de la intensidad I:

$$\begin{gathered} V_A-V_C = I · R_{1,2,3} \Rightarrow \\ 200 = I · 1130.77 \Rightarrow \\ \boxed{I = 0.18 A} \end{gathered}$$

Cuestión c)

Dado que conocemos el valor de I y de R₃, podemos aplicar nuevamente la ley de Ohm para conocer el valor de V_B-V_C:

$$\begin{gathered} V_B-V_C = I · R_3 \Rightarrow \\ {V}_B-V_C= 0.18 · 900 \Rightarrow \\ \boxed{V_B-V_C = 162 V} \end{gathered}$$

Cuestión d)

Antes de calcular, vamos a ver que ocurre con la intensidad de corriente cuando circula a través del circuito eléctrico completo:

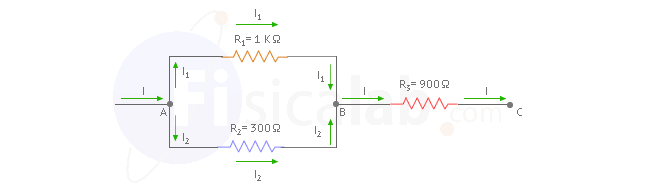
Como puedes observar, la intensidad de corriente se bifurca y se une cada vez que circula una ramificación de resistencias en paralelo. Si aplicamos la ley de Ohm para R₁, obtenemos que V_A-V_B = I₁·R₁. Conocemos R₁ y podemos calcular V_A-V_B. Pues vamos a ello...

$$\begin{gathered} V_A-V_C=(V_A-V_B)+(V_B-V_C) \Rightarrow \\ {V}_A-V_B = (V_A-V_C)-(V_B-V_C) \Rightarrow \\ {V}_A-V_B=200-162 \Rightarrow \\ {V}_A-V_B=38 V \end{gathered}$$

Aplicando la ley de Ohm sobre R₁:

$$\begin{gathered} V_A-V_B=I_1·R_1 \Rightarrow \\ {I}_1=\frac{V_A-V_B}{R_1}\Rightarrow \\ {I}_1=\frac{38}{1000}\Rightarrow \\ \boxed{I_1=0.038 A} \end{gathered}$$