Aproximación Paraxial
La aproximación paraxial se suele utilizar en el análisis de sistemas ópticos para simplificar las expresiones obtenidas y trabajar con mayor comodidad.
Los rayos de luz se encuentran en la zona paraxial cuando forman ángulos pequeños (α ≤ 10º ó α ≤ 0.1745 rad) con el eje óptico. Estos ángulos, expresados en radianes, cumplen que:
Así pues, los rayos paraxiales son los más próximos al eje óptico.
Observa que cuando hacemos cálculos en la zona paraxial el error cometido es pequeño.
Cuando un sistema óptico utiliza la aproximación paraxial, decimos que "trabaja en la zona paraxial". Gracias a esta aproximación podemos calcular la fórmula fundamental de los dioptrios esféricos y la de de los espejos esféricos de manera sencilla.
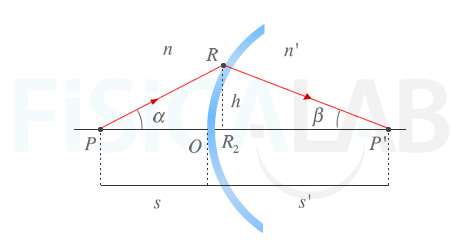
Aproximación Paraxial
Los rayos paraxiales son aquellos más próximos al eje óptico. Así, cuando los rayos se encuentran en dicha zona, la distancia entre O y la proyección de R sobre el eje (R2) se considera despreciable frente s y s'. De esta manera, podemos decir que
Se conoce como óptica gaussiana a la óptica geométrica que describe los sistemas ópticos a partir de la aproximación paraxial. Se hace así honor a Carl Friedrich Gauss, quien, en 1841, estableció la ecuación fundamental del dioptrio esférico utilizando estas aproximaciones.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
