El Espejo Plano

En óptica geométrica un espejo es cualquier superficie lisa y pulida capaz de reflejar los rayos de luz que llegan a él. El espejo refleja la luz haciendo que los rayos varíen su trayectoria y formando imágenes. En este apartado vamos a analizar como se ven las los objetos cuando estas superficies reflectoras son planas. Para ello veremos:

• Su ecuación fundamental y te mostraremos como puedes deducirla
• Qué ocurre con los focos y las distancias focales
• Si las imágenes aumentan o no respecto al objeto original
• Cuáles son y cómo puedes dibujar sus gráficas
• Qué es la inversión en profundidad
• Como se comportan los sistemas de espejos planos

¿Empezamos?

Reflejo en espejos planos

"No sé cuál es la cara que me mira cuando miro la cara del espejo" escribía Jorge Luis Borges en uno de sus poemas. Cuando termines este apartado esperamos que estés en condiciones de empezar a responder a esa pregunta, al menos desde un punto de vista físico.

Ecuación del espejo plano

Recuerda que, además del criterio DIN, existen otros criterios de signos que puedes usar, pero ambos comparten la expresión anterior.

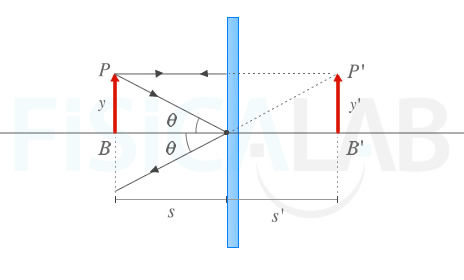
Variables de lal ecuación fundamental

La ecuación de los espejos planos establece, como se aprecia en la figura, que s y s' son iguales pero de signo contrario. De ahí, que y = y'

Comprobación

Podemos considerar la reflexión como un caso particular de refracción en el que n'=-n. Además, podemos considerar que en un espejo plano R = ∞ y usar la ecuación fundamental del dioptrio esférico. Así, nos queda:

$$\frac{n\text{'}}{s\text{'}}-\frac{n}{s}=\frac{n\text{'}-n}{R}\underset{\begin{array}{c}n\text{'}=-n\\ R=\infty \end{array}}{\underbrace{\Rightarrow }}\frac{-n}{s\text{'}}=\frac{n}{s}\Rightarrow s\text{'}=-s$$

Focos

Si observas el desarrollo para espejos esféricos, y aplicamos que R = ∞ , podemos decir:

Aumento lateral

Comprobación

A partir de la expresión del aumento lateral del dioptrio esférico, del que el espejo plano se puede considerar un caso particular, la propia ecuación fundamental del espejo plano, y asumiendo que n'=-n:

$$A_L=\frac{y\text{'}}{y}=\frac{n·s\text{'}}{n\text{'}·s}\underset{\begin{array}{c}s\text{'}=-s\\ n\text{'}=-n\end{array}}{\underbrace{=}}\frac{n·\left(-s\right)}{-n·s}=1\Rightarrow y\text{'}=y$$

Gráficas

Es habitual obtener la posición y dimensiones de las imágenes de los objetos en el espejo desde un punto de vista gráfico. Para ello se usa lo que se conoce como diagrama de rayos, como el que hemos en la figura del comienzo del apartado, que reproducimos aquí abajo. En ellos nos basta dibujar 2 rayos de trayectoria conocida, de los infinitos posibles. Te recomendamos que sigas los siguientes pasos:

1. Comienza situando el eje óptico, el objeto y el espejo
   
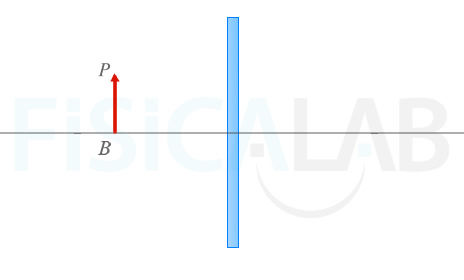
2. Traza un rayo paralelo al eje óptico desde el punto P del objeto. Dicho rayo se prolongará detrás del espejo. Utiliza puntos suspensivos para la prolongación
   
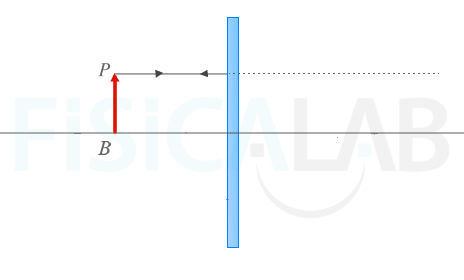
3. Traza otro rayo de la punta P al vértice óptico
   
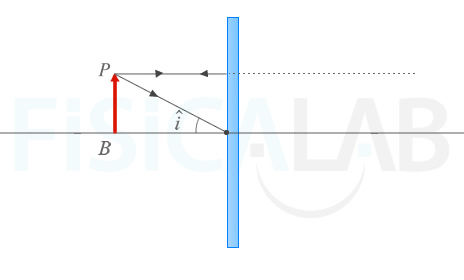
4. Dibuja el rayo reflejado. Si no cuentas con un medidor de ángulos para asegurarte que $\hat{i}={\hat{r}}_{fl}$ , puedes medir la distancia y bajo el eje óptico, para encontrar el punto auxiliar A. A partir de él, te resultará inmediato
   
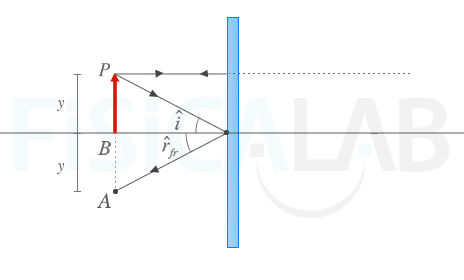
5. Prolonga hacia atrás el rayo obtenido en el apartado anterior. El punto de corte con la prolongación anterior es el punto P'
   
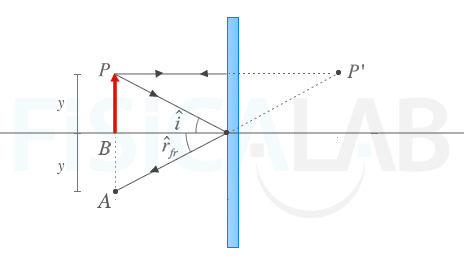
6. Proyectando P' sobre el eje óptico está B'

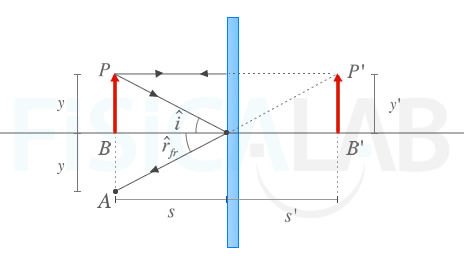
Proceso para dibujar el diagrama de rayos en un espejo plano

En los espejos planos podemos determinar la formación de la imagen con el proceso señalado en la secuencia de figuras anteriores.

Inversión en profundidad

Sitúate frente a un espejo y observa que cuando cierras, por ejemplo, tu ojo derecho, tu imagen en el espejo cierra su ojo izquierdo. Esto es fruto de la inversión en profundidad o inversión lateral que se produce en ellos.

Inversión en profundidad

Cuando le guiñas a tu imagen en el espejo, o realizas cualquier otro movimiento, se produce una inversión derecha-izquierda. Es la inversión en profundidad y ocurre para todas las imágenes formadas en el espejo.

¿Por qué ocurre este fenómeno? Matemáticamente podemos decir que el espejo transforma un sistema de coordenadas directo (esto es, ordenado según la regla de la mano derecha en el que $\overrightarrow{i}\times \overrightarrow{j}=\overrightarrow{k}$ ) a uno invertido (es decir, ordenado según una regla de la mano izquierda en la que $\overrightarrow{i}\times \overrightarrow{j}=-\overrightarrow{k}$ ).

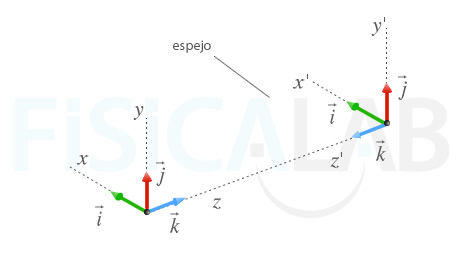
Sistema de coordenadas inversa

Dado un sistema de coordenadas rectangulares directo, el espejo lo transforma en un sistema de coordenadas inversas a través de la inversión en profundidad.

Experimenta y Aprende

Cargando...

Espejo plano. Inversión lateral

Aquí puedes observar como se comporta un espejo plano reflejando objetos. Pulsa sobre el botón play para comenzar a experimentar.

Sistemas de espejos

En el caso de que tengamos varios espejos, en lugar de uno solo, se producen varias imágenes. Uno de los casos más frecuentes se da cuando entras al probador de cualquier tienda que cuenta con un par de espejos. Vamos a estudiar el caso simple de dos espejos formando 90º entre sí.

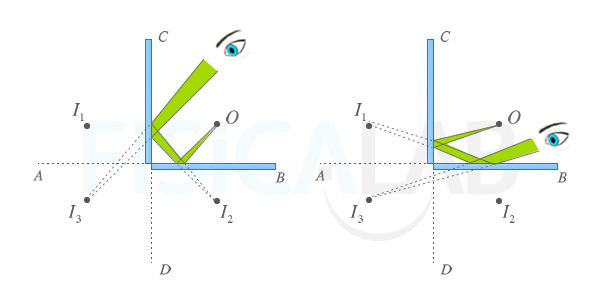
Sistema de dos espejos planos formando 90º

En la figura, un observador mira la imagen que produce un objeto O en un sistema de dos espejos, en ángulo recto, desde dos ángulos distintos. Mire desde el ángulo que mire, siempre percibe la imagen del objeto O como si proviniese de I₃.

Observa como se forman 3 imágenes distintas I₁, I₂ e I₃. La imagen I₁ se puede obtener directamente a partir del objeto O, con el procedimiento indicado para un sólo espejo, considerando el espejo C. Lo mismo ocurre con I₂ para el espejo B. En el caso de I₃, se puede considerar la imagen de I₁ en un hipotético espejo AB, pero también la imagen de I₂ en un hipotético espejo CD. En cualquier caso, la imagen real se forma por una doble reflexión de los rayos provenientes de O, tal y como se ilustra en la figura anterior.

Una importante consecuencia de esta manera de formar las imágenes es que la imagen en I₃ no presenta inversión lateral.

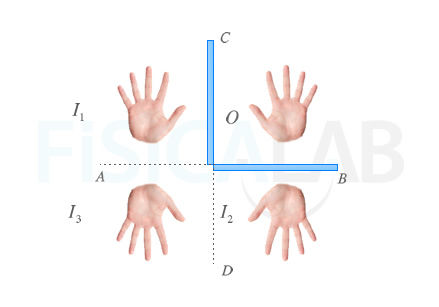
Secuencia de inversión en imagen reflejada en un sistema de dos espejos planos que forman 90º

Las imágenes I₁ e I₂ presentan inversión en profundidad, no así la imagen I₃. En el caso de la figura, el "objeto" O original es una palma de mano derecha. I₁ e I₂ , debido a la inversión lateral, son palmas de mano izquierda, mientras que I₃ vuelve a ser una palma de mano derecha