La Lupa

La lupa, también llamada microscopio simple, es un instrumento óptico que consiste en una lente convergente con una montura adecuada al fin para el que se utilizará. Su objetivo es que quién la use obtenga una visión ampliada de un objeto pequeño. Vamos a ver la lupa desde el punto de vista de la óptica geométrica, a través de los siguientes puntos:

• Funcionamiento
• Aumento angular o poder amplificador

La Lupa

La invención de la lupa es atribuida al monje franciscano Roger Bacon, en 1266. En la actualidad existen distintos tipos de lupa, adaptadas al uso que se les vaya a dar, desde las clásicas con montura circular a las lupas eléctricas

¿Ampliamos conocimientos?

Funcionamiento

El ojo humano es la base del proceso de visión. Como hemos visto, este percibe los objetos proyectando su imagen sobre la retina.

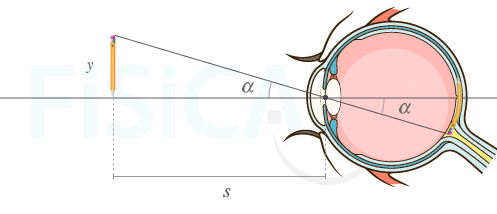
Ángulo subtendido por un objeto en la retina

Un objeto de altura y situado a una distancia s del ojo forma sobre la retina una imagen cuyo tamaño en la misma depende del ángulo α subtenido por el propio objeto.

A partir de la imagen anterior, podemos intuir que si queremos aumentar el nivel de detalle con que percibimos un objeto, debemos aumentar el ángulo α, para que la superficie de la imagen sobre la retina sea mayor. Podemos conseguir esto disminuyendo la distancia s. Sin embargo existe un límite natural impuesto a dicha distancia, el punto próximo, a una distancia x_p.

Lo que hace la lupa es, precisamente, aumentar ese ángulo. ¿Adivinas cómo? Recuerda que una lupa no es más que una lente convergente. Como pudiste observar aquí, las lentes convergentes, como por ejemplo, la biconvexa, son capaces de crear imágenes virtuales, derechas y ampliadas del objeto en cuestión, cuando este se sitúan entre el foco y la propia lente.

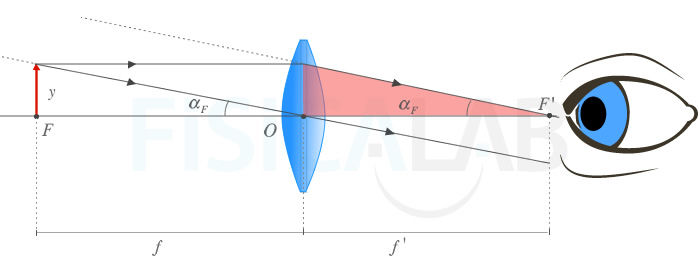
Funcionamiento de la lupa

En la imagen puedes observar como se comporta una lupa en el caso límite en el que el objeto se sitúe sobre el foco de la misma. La imagen del mismo se sitúa en el infinito ( $s\text{'}=-\infty$ ). De esta manera el ojo percibirá un objeto mayor (al ser mayor el ángulo subtendido en la retina). Además, al recibir los rayos paralelos, el ojo no se fatiga al ser innecesaria la acomodación del cristalino.

Finalmente, observa que, para que α_f > α_i , se debe cumplir que f' < x_p. Para cuantificar todas estas cuestiones de manera formal utilizamos el aumento angular o poder amplificador de la lupa.

Aumento angular

En general, decimos que el aumento angular que produce un instrumento óptico para el observador es el cociente entre el ángulo que ocupa en el campo de visión la imagen observada a través del instrumento y la imagen observada sin el instrumento óptico. Así para el caso de la lupa concretamos de la siguiente manera:

Nota: En ocasiones es posible que veas escrita la expresión anterior como $A_a=\frac{{\alpha }_f}{{\alpha }_i}=\frac{0.25}{f}$. Esta segunda forma asume el segundo criterios de signos presentado según el cual la distancia focal objeto de una lente es positiva cuando el objeto está delante de la lente, con lo que el resultado final no varía.

Observa que un aumento angular de 20 no incrementa 20 veces un objeto sino que nos permite verlo 20 veces más cerca (como si la distancia al objeto, en lugar de ser x, fuese x/20).

En general usaremos uno u otro aumento según el caso concreto estudiado. Así, al ser la lupa una lente, su aumento lateral vendría dado por A_L = s'/s, que en la disposición de la última imagen de arriba sería infinito, ya que la imagen virtual está en el infinito. Esto no significa que el objeto se vea infinitamente grande bajo la lupa. Sencillamente, cuando analizamos una lupa en esta situación, el aumento angular es útil y el transversal no.