El Dioptrio Plano

En óptica geométrica un diptrio es una superficie que separa dos medios transparentes de distinto índice de refracción. El dioptrio refracta la luz haciendo que los rayos varíen su trayectoria y formando imágenes. En este apartado vamos a analizar como se ven los objetos cuando estas superficies refractoras son planas. Para ello veremos:

• Su ecuación fundamental y como puedes deducirla
• Qué ocurre con los focos y la distancias focales
• Qué ocurre con el aumento de las imágenes

Para abordar los contenidos de este apartado cómodamente te recomendamos que antes comprendas bien el dioptrio esférico. ¿Empezamos?

Cercanía de los objetos a través del agua

El agua de un río como el de la figura es un buen ejemplo de dioptrio plano. Como estudiamos a lo largo de este apartado, en él la imagen se forma en el mismo lado que se encuentra el objeto (la trucha en este caso), y con el mismo tamaño, pero con una profundidad aparente distinta, que depende de la relación que guarden los índices de refracción de los medios (n=n_aire y n'=n_agua).

Ecuación del dioptrio plano

Despejando s' de la ecuación anterior podemos llegar a importantes conclusiones:

$$s\text{'}=s·\frac{n\text{'}}{n}$$

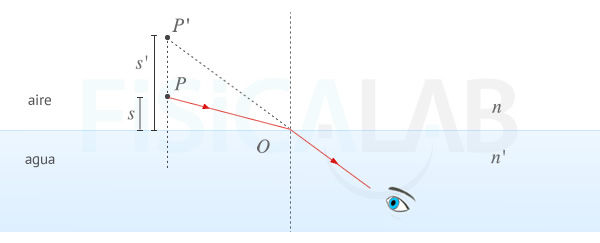
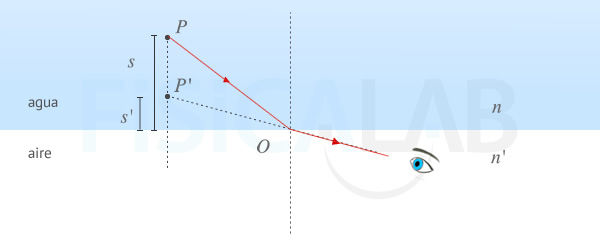
Variables de la ecuación fundamental

Las dos imágenes de la figura ilustran dos ejemplos concretos de dioptrio plano, y las variables que aparecen en la ecuación fundamental. Observa como el objeto y su imagen están siempre en el mismo lado. Observa, también, como la profundidad aparente del objeto varía, ya que el ojo sitúa su posición prolongando en linea recta, hacia atrás, los rayos que le llegan del mismo. En la imagen superior n'>n, y el objeto parece estar más lejos de lo que realmente está. En la inferior, n'<n, y el objeto parece estar más cerca de lo que realmente está.

La imagen anterior nos da la explicación óptica para entender la paradoja de las truchas, con la que abríamos el apartado: los objetos se ven más cercanos cuando están bajo agua.

¡Atención! La expresión fundamental de dioptrio plano recogida presupone el criterio de signos DIN. Bajo el otro criterio de signos presentado en el tema, la expresión queda:

$$\frac{n\text{'}}{s\text{'}}=-\frac{n}{s}$$

Comprobación

Podemos considerar la fórmula del dioptrio plano como un caso particular de la ecuación fundamental del dioptrio esférico, en el que el radio de curvatura del mismo es infinito ( R = ∞ ). Así:

$$\frac{n\text{'}}{s\text{'}}-\frac{n}{s}=\frac{n\text{'}-n}{R}\Rightarrow \frac{n\text{'}}{s\text{'}}-\frac{n}{s}=\cancel{\frac{n\text{'}-n}{\infty }}\Rightarrow \frac{n\text{'}}{s\text{'}}-\frac{n}{s}=0\Rightarrow \frac{n\text{'}}{s\text{'}}=\frac{n}{s}$$

Focos

Aunque en los dioptrios planos no tiene sentido hablar de focos como puntos reales del plano, vamos a tratar de dilucidar qué está pasando. Así, para determinar las distancias focales en el espejo plano, partiremos de la posición de los focos en el dioptrico esférico , y asumiremos que R = ∞:

$$\begin{gathered} f=-R·\frac{n}{n\text{'}-n}=-\infty \\ f\text{'}=R·\frac{n\text{'}}{n\text{'}-n}=\infty \end{gathered}$$

¡Atención! La expresión anterior se aplica al criterio DIN de signos. Para el otro criterio de signos presentado en el tema, nos quedaría:

$$f=f\text{'}=\infty$$

Aumento lateral

Para entender cómo modifican la imagen los dioptrios planos, partiremos del análisis realizado para el aumento de los dioptrios esféricos.

Comprobación

Usaremos la expresión del aumento lateral del dioptrio esférico y la propia ecuación fundamental del drioptrio plano:

$$\begin{gathered} A_L=\frac{y\text{'}}{y}=\frac{n·s\text{'}}{n\text{'}·s} ;\hspace{0.17em} \\ \frac{n\text{'}}{s\text{'}}=\frac{n}{s}\Rightarrow n\text{'}·s=s\text{'}·n; \Rightarrow A_L=1 \end{gathered}$$