Lentes Delgadas
Los sistemas ópticos más utilizados en la actualidad son las lentes. Estas forman pate de gafas, cámaras fotográficas, prismáticos y un largo etcétera. En este apartado vamos a estudiarlas a la luz de la óptica geométrica. Para ello veremos:
- Como se definen
- Sus principales tipos
- La ecuación fundamental de las lentes delgadas
- Cómo determinar su foco
- Cómo determinar su aumento lateral
- Qué es la potencia de una lente y qué son las dioptrías
- Qué pasos hay que seguir para su representación gráfica
¿Preparado?
Definición
Una lente es un sistema óptico constituido por un medio transparente que se encuentra limitado por dos superficies refractarias o dioptrios de las que, al menos una, está curvada.

Etimología de la palabra lente
La palabra lente proviene del latín lens, lentis que significa lenteja. ¿Imaginas el porqué?
Las lentes ópticas son conocidas desde la antigüedad: Aristófanes en su obra Las nubes (423 a.C.) menciona el uso de las mismas para enfocar rayos del Sol y fundir cera. Sin embargo, es el conocimiento de los principios ópticos a partir del S. XV lo que permite desarrollarlas según el fin concreto al que se destinen.
Para el estudio de las lentes nos centraremos en el caso de que el índice de refracción de la misma es mayor que el del medio que la rodea.
Tipos
Podemos clasificar las lentes atendiendo a distintos criterios:
- Grosor: Decimos que hay lentes delgadas y lentes gruesas según tengan un grosor pequeño o alto respectivamente en comparación con los radios de curvatura de las superficies refractoras y con las distancias s y s'. De ahora en adelante nos centraremos en las lentes delgadas
-
Comportamiento: Decimos que hay lentes convergentes (también llamadas convexas o positivas) y lentes divergentes (también llamadas cóncavas o negativas). Las primeras hacen converger ("unen") los rayos que llegan paralelos al eje óptico en un punto denominado foco imagen, a la derecha de la lente. En las segundas los rayos divergen ("se separan") al pasar por la lente, por lo que el foco imagen se sitúa a la izquierda de la lente, dónde convergen las prolongaciones de los rayos.
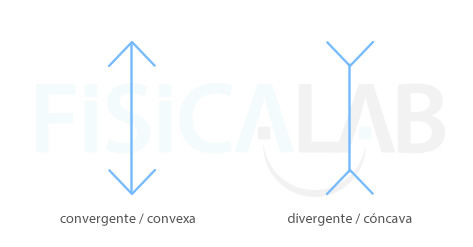
Simbolos simplificados para las lentes
Es habitual representar las lentes mediante una línea vertical y dos flechas cuyo sentido determina si se trata de una lente convergente o divergente.
- Forma: Podemos hacer una clasificación atendiendo al valor de los radios de curvatura de los dos dioptrios que componen la lente:
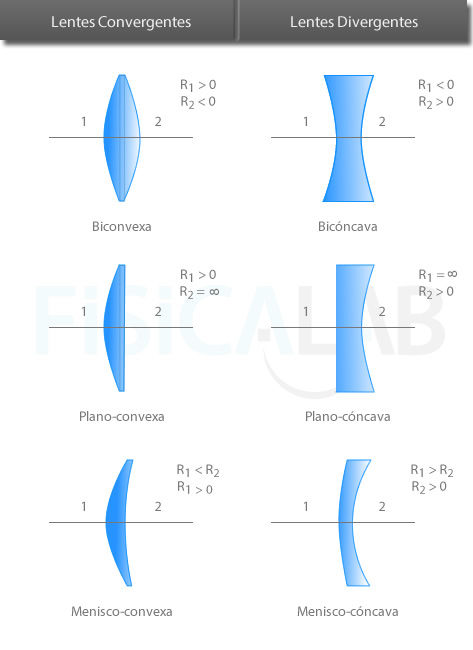
Clasificación de las lentes delgadas atendiendo a su forma.
Observa como las lentes convergentes son más gruesas en su parte central y las divergentes son más gruesas en sus extremos. Por otro lado, las lentes menisco-convexa y menisco-cóncava también se suelen denominar menisco-convergente y menisco-divergente respectivamente. Los signos de los radios indicados corresponden al criterio DIN.
El comportamiento convergente o divergente de una lente depende, en realidad, de la relación entre el índice de refracción del medio que rodea la lente,n , y el de la propia lente, n'. Cuando decimos con carácter general que una lente es convergente o divergente lo hacemos asumiendo que n'>n , y más concretamente, que la lente se encuentra en el aire ( n=1 ).
Ecuación fundamental
La ecuación fundamental de las lentes delgadas, también conocida como ecuación del fabricante de lentes o ecuación del constructor de lentes, es una igualdad que relaciona la distancia a la lente del objeto y de la imagen con los índices de refracción de la lente y del medio en el que se encuentra según:
Donde:
- n' y n : Índices de refracción de la lente y del medio en que se encuentra respectivamente. Es una magnitud adimensional
- s , s' : Son las distancias del objeto y la imagen respectivamente al origen O, situado en el centro de la lente. Su unidad de medida en el Sistema Internacional (S.I.) es el metro (m). Según el criterio DIN de signos, que usamos, son negativas cuando están delante de la lente y positivas detrás
- R1 y R2 : Son los radios de curvatura de la primera y de la segunda superficie refractara de la lente respectivamente. Su unidad de medida en el S.I. es el metro (m)
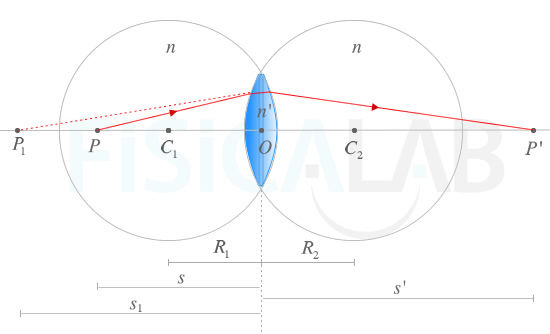
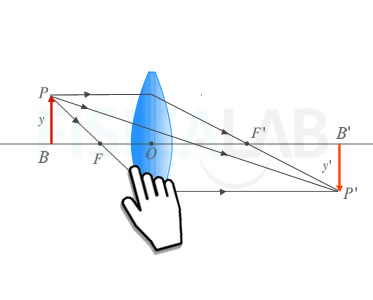
Variables de la ecuación fundamental
En la imagen están representadas las variables que aparecen en la ecuación fundamental de la lente delgada. Los rayos procedentes del punto P se enfocan en el punto P'. La lente funciona como dos dioptrios de radios R1 y R2 respectivamente de manera que la imagen producida por el primero de ellos, P1, actúa como objeto para el segundo.
¡Atención! La expresión anterior presupone el criterio de signos DIN. Es habitual que encuentras también la siguiente:
Esta última expresión asume el segundo criterio de signos que te presentamos, en el que s es positivo para los objetos reales, es decir, situados delante de la lente y el resto de magnitudes coinciden en signo.
Comprobación
Para obtener la fórmula anterior, partimos del caso particular de la lente biconvexa de la imagen anterior. Al ser una lente delgada, podemos despreciar el grosor de la misma y situar el origen del sistema óptico en el centro de la propia lente. De esta manera, los rayos procedentes del punto P, que se encuentra a una distancia s del origen se refractan en primer lugar en la superficie de radio R1 y forman una imagen en el punto P1, a una distancia s1 del origen. La ecuación fundamental del dioptrio nos da la siguiente relación:
Siguiendo su camino en el interior de la lente, los rayos alcanzan el dioptrio de radio R2. Para este, los rayos parecen provenir de P1, que actúa esta vez como objeto. Así pues, tras refractarse, forman la imagen de P1 en el punto P', a una distancia s' del origen. La ecuación fundamental arroja, en este caso, la siguiente igualdad:
Sumando las dos ecuaciones anteriores, llegamos a la fórmula de las lentes delgadas:
La expresión anterior puede ser reescrita si la lente se encuentra en aire ( n = 1 ) según:
Ten presente que, aunque hemos llegado a la expresión buscada considerando una lente biconvexa, su forma es igualmente válida para el resto de tipos de lentes delgadas, sin más que considerar los signos adecuados para R1 y R2.
Focos
Existen dos puntos muy importantes cuando estudiamos una lente delgada: su foco objeto y su foco imagen.
- El foco objeto F es el punto en el que hay que colocar el objeto para que los rayos salgan paralelos de la lente. A la distancia entre el origen y el foco objeto se la denomina distancia focal objeto f. Matemáticamente,
- El foco imagen F' es el punto en el que convergen los rayos provenientes del infinito, es decir, aquellos que llegan a la lente paralelos al eje óptico. A la distancia entre el origen y el foco imagen se la denomina distancia focal imagen f'. Matemáticamente,
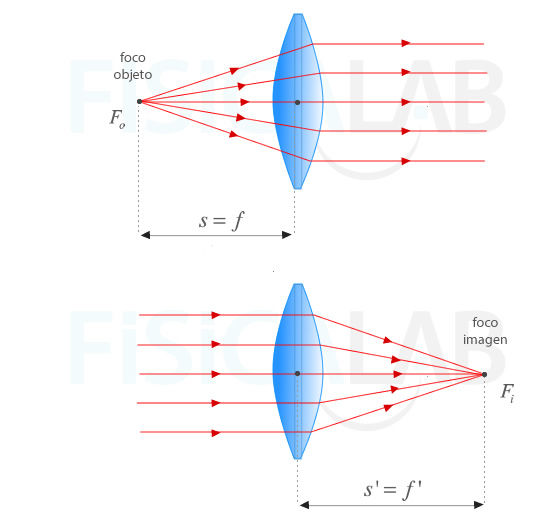
Focos en lentes delgadas
Arriba, los rayos procedentes de un objeto situado a una distancia s=f del origen salen paralelos al eje óptico ( s'=∞ ). Abajo, los rayos provenientes del infinito ( s=-∞ ) convergen en el foco imagen, a una distancia s'=f' del origen.
Podemos reescribir la ecuación del constructor del lentes en función de la distancia focal objeto e imagen según:
Donde:
- n' y n : Índices de refracción de la lente y del medio en que se encuentra respectivamente. Es una magnitud adimensional
- f, f' : Distancia focal objeto e imagen respectivamente. La unidad de medida de ambas en el Sistema Internacional (S.I.) es el metro ( m )
- R1 y R2 : Son los radios de curvatura de la primera y de la segunda superficie refractara de la lente respectivamente. Su unidad de medida en el S.I. es el metro (m)
De lo anterior es inmediato:
¡Atención! Las expresiones anteriores siguen el criterio de signos DIN. Si siguiéramos el otro criterio de signos presentado en el tema, obtendríamos:
Comprobación
Partiendo de la propia definición dada para las distancias focales y sustituyendo en la ecuación fundamental obtenemos:
La fórmula gaussiana de las lentes delgadas establece la siguiente relación:
Observa que, para desarrollar la identidad anterior, basta considerar la ecuación fundamental y la ecuación del constructor de lentes en función de las distancias focales en el caso en que el medio en el que se encuentra la lente es el aire (n = 1).
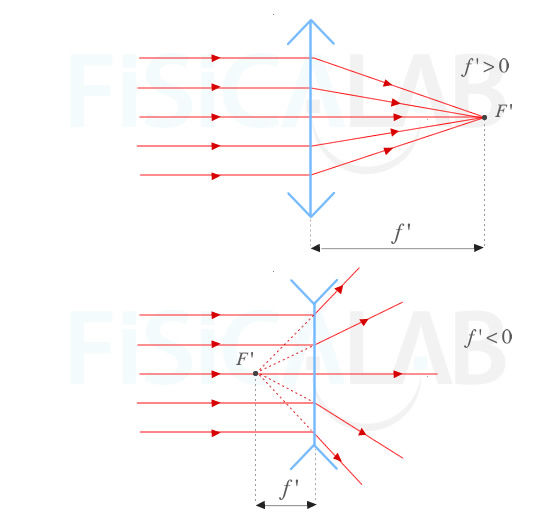
Signos distancia focal en lentes convergentes y divergentes
En la figura superior tienes una lente convergente. En ellas el foco imagen se encuentra a la derecha. Por el contrario, en la figura inferior aparece una lente divergente, en las que el foco imagen se encuentra a la izquierda.
La ecuación gaussiana pone claramente de manifiesto que sólo las lentes convergentes producen imágenes reales (a la derecha de la lente). Efectivamente:
Para que la imagen sea real se debe cumplir, según criterio DIN, que s' > 0, y por tanto 1/s' > 0. Dado que lo habitual es colocar el objeto a la izquierda de la lente, 1/s < 0, y por tanto la única posibilidad de que 1/s' > 0 es que 1/f' > 0. Esto solo ocurre en las lentes convergentes. Podrás comprobar este punto en el Experimenta y aprende más abajo.
¡Atención! Si en lugar del criterio de signos DIN se utiliza el otro criterio de signos presentado para superficies refractaras, el foco objeto y el foco imagen tienen igual signo, f=f' y la fórmula gaussiana queda:
Es muy habitual encontrar escrita la fórmula del constructor de lentes a partir de la distancia focal y considerando n=1.
- Según criterio DIN:
- Según el otro criterio considerado:
A pesar de que hemos presentado distintas expresiones en este apartado, no te dejes confundir: en la práctica basta recordar la ecuación fundamental y las definiciones de foco objeto y foco imagen para llegar de unas a otras.
Aumento lateral
La imagen de los objetos puede resultar aumentada o disminuida respecto al objeto original tras atravesar una lente.
Se define el aumento lateral o aumento transversal de la imagen, y se denota AL , como la relación entre la altura de esta, y', y la altura del propio objeto, y, según:
Recuerda que el aumento lateral es una magnitud dimensional que te va a permitir, conocida la altura del objeto original o de la imagen, determinar la altura del otro. Además:
- Si |AL| > 1 , el tamaño de la imagen es mayor que el del objeto
- Si |AL| < 1 , el tamaño de la imagen es menor que el del objeto
- Si AL > 0 , la imagen es derecha y en el mismo lado de la lente que el objeto (imagen virtual)
- Si AL < 0 , la imagen está invertida y en el lado contrario que el objeto (imagen real)
¡Atención! La expresión anterior presupone el criterio de signos DIN. Bajo el otro criterio de signos presentado, nos queda:
Comprobación
Observa la siguiente figura:
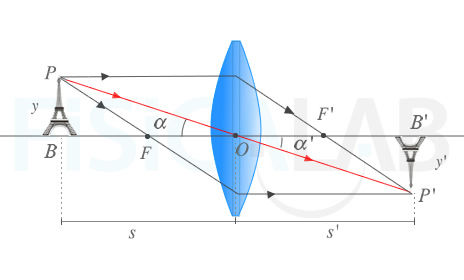
Deducción aumento lateral
La torre Eiffel, a la izquierda de la imagen, representa un objeto de altura y cuya imagen tendrá una altura y', en general, diferente, que dependerá del aumento lateral. En las lentes delgadas el rayo que pasa por el centro óptico de la lente, representado en rojo, no modifica su trayectoria y lo utilizaremos para comprobar la expresión del aumento transversal.
Siendo coherentes con el criterio de signos usado, también para los ángulos, podemos comenzar diciendo que:
Por otro lado, asumiendo la aproximación paraxial:
Potencia y dioptrías
La potencia de una lente, P, representa la capacidad de una lente para hacer converger los rayos de luz que la atraviesan. Se define como la inversa de la distancia focal imagen, f':
Su unidad de medida en el Sistema Internacional (S.I.) es el metro elevado a menos uno ( m-1)
Observa que el signo de la potencia coincide con el de f', de ahí que sea negativa en una lente divergente. Por otro lado, el valor concreto de la misma está fuertemente relacionado con las característica físicas de la lente. Expresando la potencia según:
puedes ver que la potencia aumenta cuando mayor es el índice de refracción de la lente y cuanto menores sean sus radios de curvatura.
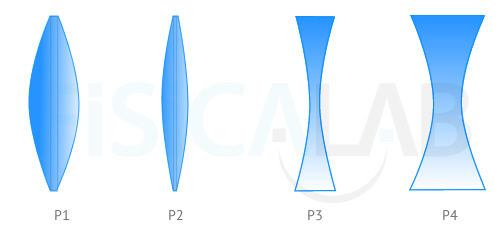
Potencia en lentes
Observa que, suponiendo que todas las lentes de la figura tienen igual índice de refracción, las de los extremos tienen el mayor valor absoluto de potencia, al tener los radios mayores. Además, las dos lentes convergentes de la izquierda tienen una potencia positiva, frente a las dos lentes de la derecha, divergentes, y con potencia negativa. Se cumple que P1 > P2 > P3 > P4.
Es muy común utilizar la dioptría, D, como unidad de medida de la potencia de una lente. Una dioptría es la potencia de una lente cuya distancia focal es de un metro, por tanto, siempre que expreses la distancia focal imagen en metros, la potencia la obtendrás en dioptrías.
Gráficas
Podemos obtener la posición y dimensiones de las imágenes de los objetos en la lente desde un punto de vista gráfico. Como ya hemos visto para los dioptrios y los espejos, usaremos lo que se conoce como diagrama de rayos. En ellos nos basta dibujar 2 rayos de trayectoria conocida, de los infinitos posibles. En realidad, es fácil dibujar al menos tres.
Se denominan rayos principales a rayos de trayectoria conocida que nos permiten determinar la posición de la imagen de un objeto en un diagrama de rayos. En el espejo esférico son:
- El rayo procedente del objeto y paralelo al eje óptico, que, tras refractarse en la lente, pasará por el foco imagen
- El rayo que, procedente del objeto, pasa por el centro óptico de la lente. Tras refractarse en la lente no modificará su dirección
- El rayo procedente del objeto que pase por el foco objeto, que, tras refractarse en la lente, saldrá paralelo al eje óptico
Observa que ya hemos visto a lo largo de este tema varios diagramas de rayos. Aquí tienes dos ejemplos más con los que ilustramos los rayos principales de la lente delgada:
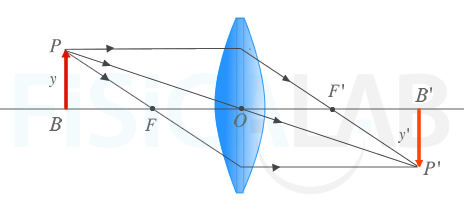
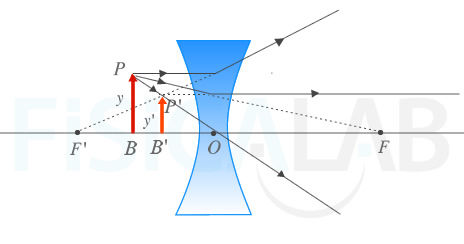
Diagramas de rayos en lentes convergentes y divergentes
La imagen superior representa un diagrama de rayos de una lente delgada convergente. En la parte inferior, una lente delgada divergente.
Aunque no se considera un rayo principal, el rayo que coincide con el eje óptico tampoco modifica su dirección y nos sirve para determinar la base de la imagen del objeto.
Para dibujar un diagrama de rayos de una lente delgada:
- Comienza dibujando el eje óptico y la lente delgada en el origen. Para simplificar, puedes utilizar la representación con flechas indicada más arriba según la lente sea convergente o divergente
- Sitúa el objeto
- Identifica el foco objeto F y el foco imagen F'
- Traza al menos 2 de los rayos principales de la punta P del objeto
- El punto de intersección de los rayos es P', la imagen del punto P
- Proyecta P' sobre el eje óptico para obtener la base de la imagen del objeto, B'
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.