El Dioptrio Esférico

En óptica geométrica un diptrio es una superficie que separa dos medios transparentes de distinto índice de refracción. El dioptrio refracta la luz haciendo que los rayos varíen su trayectoria y formando imágenes. En este apartado vamos a analizar como se ven los objetos cuando estas superficies refractoras son esféricas, y lo haremos bajo la aproximación paraxial. Para ello veremos:

• Su ecuación fundamental y te mostraremos como puedes deducirla
• El concepto de foco
• Como aumentan o disminuyen las imágenes
• Cuáles son y cómo puedes dibujar sus gráficas

¿Empezamos?

Ecuación del dioptrio esférico

La ecuación fundamental del dioptrio esférico es una igualdad que relaciona, bajo aproximación paraxial, la distancia al origen del objeto y la de la imagen con los índices de refracción de los medios y el radio de curvatura del dioptrio según:

$$\frac{n\text{'}}{s\text{'}}-\frac{n}{s}=\frac{n\text{'}-n}{R}$$

Donde:

• n y n' : Índices de refracción de los medios 1 y 2 respectivamente. Es una magnitud adimensional
• s , s' : Son las distancias del objeto y la imagen respectivamente al origen O, situado en el vértice óptico. Su unidad de medida en el Sistema Internacional (S.I.) es el metro (m). Según el criterio DIN de signos, que usamos, son negativas cuando están delante del dioptrio y positivas detrás

• R : Es el radio de curvatura del dioptrio esférico. Su unidad de medida en el S.I. es el metro (m). Según el criterio DIN:

  • Dioptrio convexo → R > 0 
  • Dioptrio cóncavo → R < 0 

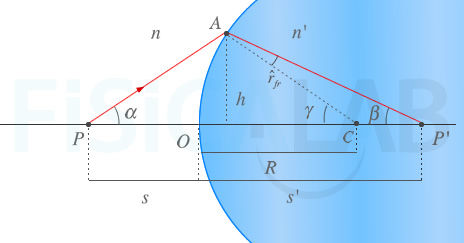
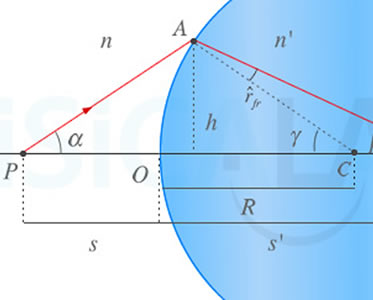
Variables de la ecuación fundamental

En la imagen, un esquema de un dioptrio esférico convexo en el que se aprecian las variables que aparecen en la ecuación fundamental. El rayo saliente del punto P se enfoca en el punto imagen P'.

¡Atención! La expresión anterior presupone el criterio de signos DIN. Es habitual que encuentres también la siguiente:

$$\frac{n\text{'}}{s\text{'}}+\frac{n}{s}=\frac{n\text{'}-n}{R}$$

Esta última expresión asume el segundo criterio de signos que te presentamos, en el que s es positivo para los objetos reales, es decir, situados delante del dioptrio y el resto de magnitudes coinciden en signo.

Comprobación

En este desarrollo nos basaremos en la imagen anterior. Partiendo de la ley de Snell de la refracción podemos encontrar la relación entre $\hat{i}$  y ${\hat{r}}_{fr}$ . Si, además, aplicamos la aproximación paraxial, nos queda:

$$n·\sin \left(\hat{i}\right)=n\text{'}·\sin \left({\hat{r}}_{fr}\right)\Rightarrow n·\hat{i}=n\text{'}·{\hat{r}}_{fr}$$

Por otro lado, nos conviene recordar la relación que existe entre el ángulo exterior a cualquier triángulo y los internos no adyacentes, tal como se recoge en la siguiente figura:

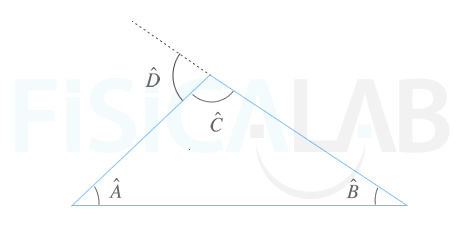
Relación del ángulo exterior a cualquier triángulo.

$$\begin{gathered} \left.\begin{array}{r}\hat{A}+\hat{B}+\hat{C} = 180º\\ \hat{C}+\hat{D} =180º\end{array}\right\} \Rightarrow \hat{A}+\hat{B}+\cancel{\hat{C}} =\cancel{\hat{C}}+\hat{D} \Rightarrow \\ \boxed{\hat{D}=\hat{A}+\hat{B} } \end{gathered}$$

Cualquier ángulo exterior a un triángulo es igual a la suma de los ángulos internos opuestos.

Teniendo en cuenta que, según el criterio DIN, α es negativo, y son positivos $\hat{i} , {\hat{r}}_{fr} , \beta , \gamma$ , podemos escribir:

• $\left|\hat{i}\right|=\left|\alpha \right|+\left|\gamma \right|\Rightarrow \hat{i}=-\alpha +\gamma$
• $\left|\gamma \right|=\left|{\hat{r}}_{fr}\right|+\left|\beta \right|\Rightarrow \gamma ={\hat{r}}_{fr}+\beta \Rightarrow {\hat{r}}_{fr}=\gamma -\beta$

Sustituyendo en la ley de Snell, nos queda:

$$n·\left(\gamma -\alpha \right)=n\text{'}·\left(\gamma -\beta \right)\Rightarrow n\text{'}·\beta -n·\alpha =\left(n\text{'}-n\right)·\gamma$$

Llegados a este punto, hay que tener presente que la aproximación paraxial supone rayos muy próximos al eje óptico. Tanto, que podemos considerar que el pie de la vertical del punto A coincide con O, por lo que:

$$\tan \left(\alpha \right)\simeq \alpha \simeq \frac{h}{s} ;\hspace{0.17em}\tan \left(\gamma \right)\simeq \gamma \simeq \frac{h}{R} ;\hspace{0.17em}\tan \left(\beta \right)\simeq \beta \simeq \frac{h}{s\text{'}}$$

Sustituyendo en la ecuación anterior y simplificando nos queda la ecuación buscada:

$$\frac{n\text{'}}{s\text{'}}-\frac{n}{s}=\frac{n\text{'}-n}{R}$$

Focos

Existen dos puntos muy importantes cuando estudiamos un dioptrio: su foco objeto y su foco imagen.

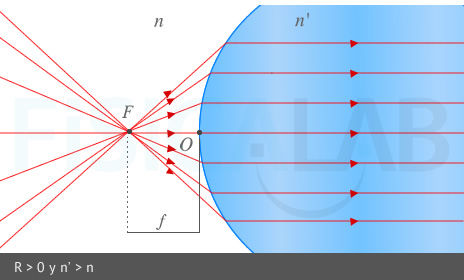
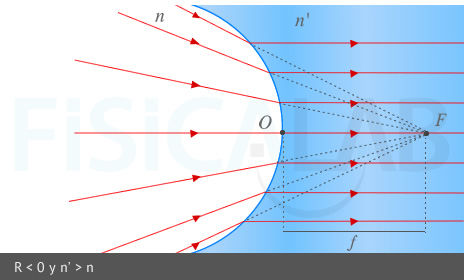
Foco objeto y distancia focal objeto.

Los rayos que pasan por el foco F, a una distancia f del vértice u origen O del diptrio, salen paralelos al eje óptico tras refractarse en este. En la primera imagen tenemos un dioptrio esférico convexo (R > 0) ⇒ f < 0 (lado izquierdo del dioptrio). En la segunda imagen tenemos un dioptrio esférico cóncavo (R < 0 ) ⇒ f > 0 (lado derecho del dioptrio)

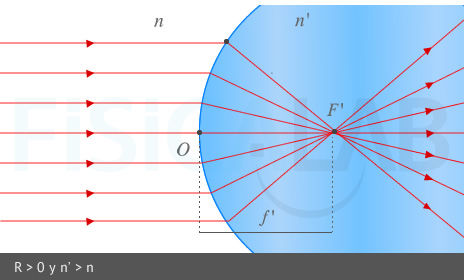
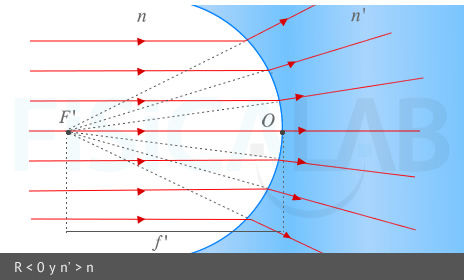
Foco imagen y distancia focal imagen.

Los rayos provenientes del infinito, paralelos al eje óptico, convergen todos en el foco F', a una distancia f' del vértice u origen O del diptrio, tras refractarse en este. En la imagen superior tenemos un dioptrio esférico convexo (R > 0) ⇒ f' > 0 (lado derecho del dioptrio). En la imagen izquierda tenemos un dioptrio esférico cóncavo (R < 0 ) ⇒ f'<0 (lado izquierdo del dioptrio)

Puesto que f y f' son distancias, seguimos para ellas el mismo criterio de signos que para s y s' respectivamente.

¡Atención! La expresión para la distancia focal objeto presupone el criterio de signos DIN. Es habitual que encuentras también la siguiente:

$$f=R·\frac{n}{n\text{'}-n}$$

Esta última expresión asume el segundo criterio de signos que te presentamos, en el que f debe ser positivo para los objetos reales, es decir, situados delante del dioptrio, y el resto de magnitudes coinciden en signo. Por contra, la expresión de la distancia focal imagen es válida para cualquiera de los dos convenios de signos presentados en el tema.

Características

Las dos expresiones presentadas nos permiten llegar a algunas relaciones interesantes:

• Si dividimos f entre f':

  $$\frac{f}{f\text{'}}=\frac{n}{n\text{'}}$$

  En donde se observa que las distancias focales son directamente proporcionales a sus respectivos índices de refracción. También puedes deducir que la distancia focal es mayor, en valor absoluto, en el medio que tenga mayor índice de refracción

• Si sumamos f con f' :

  $$f+f\text{'}=R$$

  Es decir, la suma de las distancias focales es igual al radio de curvatura

• Si dividimos los dos miembros de la ecuación fundamental del dioptrio esférico entre el segundo, obtenemos la ecuación de Gauss:

  $$\frac{f\text{'}}{s\text{'}}+\frac{f}{s}=1$$

Comprobaciones

Aunque hasta ahora hemos presentado muchas fórmulas distintas, lo cierto es que todas parten de la ecuación fundamental. Así, podemos deducir la ecuación de la distancia focal objeto recordando que los rayos deben salir paralelos al eje óptico, lo que significa que s'=∞. Para ese valor de s', s=f , con lo que:

$$\cancel{\frac{n\text{'}}{\infty }}-\frac{n}{f}=\frac{n\text{'}-n}{R}\Rightarrow f=-R·\frac{n}{n\text{'}-n}$$

Por otro lado, podemos deducir la ecuación de la distancia focal imagen recordando lo qué significa que los rayos incidan paralelos al eje óptico, que s=-∞. Para ese valor de s, s'=f' , con lo que:

$$\frac{n\text{'}}{f\text{'}}-\cancel{\frac{n}{-\infty }}=\frac{n\text{'}-n}{R}\Rightarrow f\text{'}=R·\frac{n\text{'}}{n\text{'}-n}$$

Aumento lateral

La imagen de los objetos puede resultar aumentada o disminuida respecto al objeto original tras refractarse en la superficie transparente.

El aumento lateral es una magnitud adimensional que permite, conocida la altura del objeto original o de la imagen, determinar la altura del otro.

• Si |A_L| > 1 , el tamaño de la imagen es mayor que el del objeto
• Si |A_L| < 1 , el tamaño de la imagen es menor que el del objeto
• Si A_L > 0 , la imagen es derecha
• Si A_L < 0 , la imagen está invertida

¡Atención! La expresión anterior presupone el criterio de signos DIN. Bajo el otro criterio de signos presentado, nos queda:

$$A_L=\frac{y\text{'}}{y}=-\frac{n·s\text{'}}{n\text{'}·s}$$

Comprobación

Para la demostración nos valdremos de la siguiente figura:

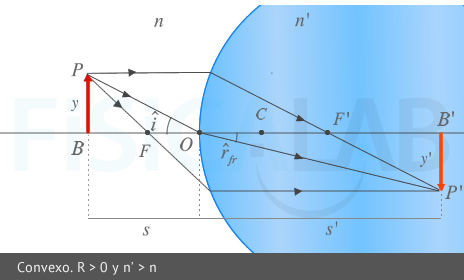
Aumento lateral.

La punta de flecha, a la izquierda de la imagen, representa un objeto de altura y cuya imagen tendrá una altura y', en general, diferente, que dependerá del aumento lateral del dioptrio.

A partir del rayo que sigue la trayectoria POP', y utilizando la aproximación paraxial, podemos escribir:

$$\sin \left(\hat{i}\right)\simeq \hat{i}\simeq \tan \left(\hat{i}\right)=\frac{y}{s} ; \sin \left({\hat{r}}_{fr}\right)\simeq \hspace{0.17em}{\hat{r}}_{fr}\simeq \tan \left({\hat{r}}_{fr}\right)=\frac{y\text{'}}{s\text{'}}$$

Por otro lado, La ley de Snell bajo aproximación paraxial nos dice que:

$$n·\hat{i}=n\text{'}·{\hat{r}}_{fr}\Rightarrow n·\frac{y}{s}=n\text{'}·\frac{y\text{'}}{s\text{'}}\Rightarrow \frac{y\text{'}}{y}=\frac{n·s\text{'}}{n\text{'}·s}=A_L$$

Gráficas

Es habitual obtener la posición y dimensiones de las imágenes de los objetos en el dioptrio desde un punto de vista gráfico. Para ello se usa lo que se conoce como diagrama de rayos. En ellos nos basta dibujar 2 rayos de trayectoria conocida, de los infinitos posibles. En realidad, es fácil dibujar al menos tres.

Observa que ya hemos visto a lo largo de este tema algunos diagramas de rayos. Aquí tienes dos ejemplos más:

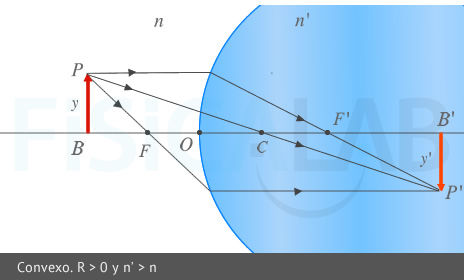
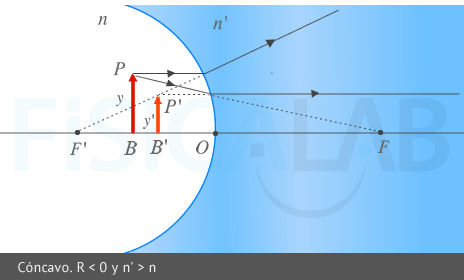
Diagrama de rayos

La imagen superior representa un diagrama de rayos en el que un dioptrio convexo ( R > 0 ) forma una imagen del objeto real e invertida. La imagen inferior representa un diagrama de rayos en el que un dioptrio cóncavo ( R < 0 ) forma una imagen del objeto virtual y derecha.

Para dibujar un diagrama de rayos de un dioptrio esférico:

1. Comienza situando el eje óptico, el objeto y el dioptrio
2. Identifica los focos F y F' (y opcionalmente el centro C) del dioptrio
3. Traza al menos 2 de los rayos principales de la punta P del objeto
4. El punto de intersección de los rayos es P', la imagen del punto P
5. Proyecta P' sobre el eje óptico para obtener la base de la imagen del objeto, B'

Experimenta y Aprende

Cargando...

Sistema óptico con dioptrio

Aquí puedes simular como se comporta un sistema óptico formado por un dioptrio. Pulsa sobre el botón play para comenzar a experimentar.