Descomposición de Fuerzas

En ocasiones, a la hora de estudiar la fuerza que actúa sobre un cuerpo, puede ser interesante descomponerla en varias fuerzas cada una de ellas con la dirección de los ejes cartesianos, de tal forma que el efecto de todas ellas sea equivalente a la fuerza descompuesta. Tal y como estudiamos en el apartado de representación de vectores, en el plano OXY obtenemos que:

$$\overrightarrow{F}=\overrightarrow{F_x}+\overrightarrow{F_y}=F_x·\overrightarrow{i}+F_y·\overrightarrow{j}$$

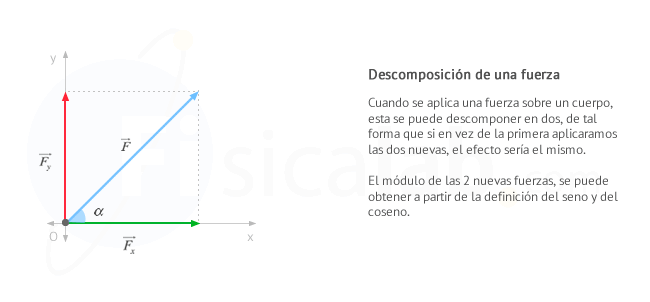
Teniendo en cuenta la definición de módulo de un vector, el módulo de la fuerza $\overrightarrow{F}$ se obtiene mediante la siguiente expresión:

$$F=\sqrt{{F_x}^2+{F_y}^2}$$

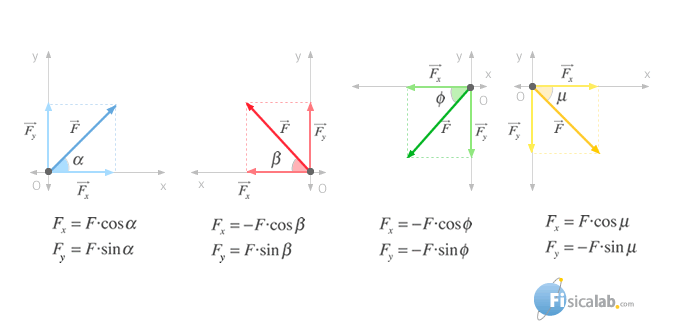
Y por medio de la definición de tangente de un ángulo agudo, podemos relacionar los módulos F_x y F_y con el ángulo α que forma $\overrightarrow{F}$ con el semieje X positivo de la siguiente forma:

$$\tan \left(\alpha \right)=\frac{F_y}{F_x}$$

Adicionalmente podemos relacionar estos módulos con el menor ángulo que forma $\overrightarrow{F}$ con el eje X, atendiendo al cuadrante del sistema de referencia en el que se encuentre: