Ángulos

Antes de comenzar a adentrarnos en el mundo de la trigonometría, debemos presentarte a su principal protragonista, los ángulos. Lo haremos a través de los siguientes puntos:

• El concepto de ángulo
• El convenio utilizado habitualmente para definir el signo de los ángulos
• Las unidades en que medimos los ángulos
  • Sistema sexagesimal
  • Sistema centesimal
  • Radianes
• Cómo convertir de grados sexagesimales a radianes y viceversa
• Como transformar un ángulo a su equivalente en el primer giro
• Clasificaciones de ángulos

Concepto de ángulo

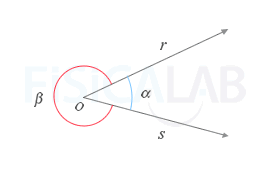
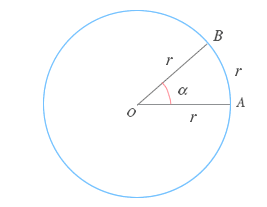
Un ángulo en un plano es cualquiera de las dos regiones que quedan separadas por dos semirectas que poseen un origen común. Ambas semirrectas reciben el nombre de lados y el origen común el nombre de vértice. 

Definición de Ángulo

Si dibujas dos semirrectas (r y s) que parten de un mismo origen (O) provocarás la aparición de dos regiones que quedan determinadas cada una de ellas por un ángulo (α y β). Por norma general los ángulos se suelen representar como un arco entre los segmentos acompañado de una letra del alfabeto griego ( α, β, ...) o la letra del vértice con un acento circunflejo ( Ô )

Criterio de orientación de ángulos

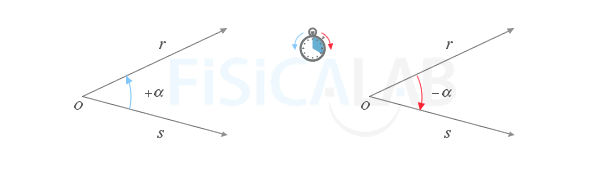
Aunque te resulte algo extraño, los ángulos pueden representarse como ángulos positivos o ángulos negativos.  Dicho valor se obtiene dependiendo del sentido que se utlice al girar una de las dos semirrectas ( semirrecta origen ) sobre la otra ( semirrecta extremo ). De esta forma, 

• Un ángulo es positivo si el giro de la semirrecta origen sobre la destino se realiza en sentido contrario de las agujas de un reloj analógico.
• Un ángulo es negativo si el giro de la semirrecta origen sobre la destino se realiza en el sentido de las agujas de un reloj analógico.

Ángulos positivos y negativos

El ejemplo de la figura si arrastramos s sobre r siguiendo el sentido contrario de las manecillas del reloj , el ángulo que representa el área encerrada entre ambas semirrectas se considera positivo. Si por el contrario lo hacemos en el sentido de las agujas del reloj, el ángulo se considera negativo.

Unidades de ángulos

Para determinar la amplitud de un ángulo, o lo que es lo mismo medirlo, suelen utilizarse distintas unidades, cada una asociada a un sistema de medida diferente. En concreto, las más utilizadas son los grados sexagesimales, los grados centesimales y los radianes. Todas ellas se basan en el concepto de ángulo completo, es decir el mayor ángulo que existe entre una semirrecta y ella misma.

Ángulo completo

El ángulo completo es el que corresponde a la circunferencia completa.

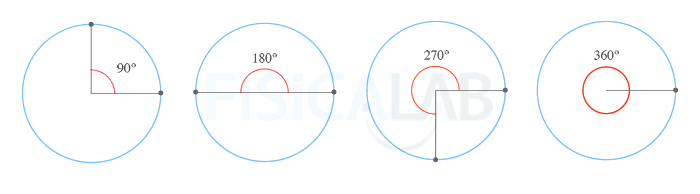
Sistema sexagesimal

En este sistema se divide un ángulo completo, o lo que es lo mismo, una circunferencia completa, en 360 partes iguales por medio de segmentos que poseen como origen común el radio de dicha circunferencia. El ángulo determinado por cada región recibe el nombre de grado sexagesimal (1º). Cada grado a su vez se divide en 60 minutos (60 ') y cada minuto en 60 segundos (60''):

1º = 60 '
1' = 60 ''

Por tanto, en el sistema sexagesimal un ángulo completo está formado por 360º o 21600' o 1296000 ''

Principales ángulos en grados sexagesimales

Como puedes observar, en este sistema el ángulo recto corresponde a 90º y el llano a 180º.

Conversión entre forma decimal y grados, minutos y segundos

Si quieres convertir un ángulo en grados sexagesimales, por ejemplo de 45.78º, expresado con decimales, a su forma en grados, minutos y segundos:

• La parte entera es directamente el número de grados. En nuestro ejemplo, 45º
• Multiplicamos la parte decimal por 60. En nuestro ejemplo, 0.78·60 = 46.8. La parte entera que nos queda es el número de minutos. En nuestro ejemplo 46'
• Multiplicamos la parte decimal restante por 60. En nuestro ejemplo, 0.8·60 = 48. La parte entera que nos queda es el número de segundos. En nuestro ejemplo 48''

Por tanto, 45.78º = 45º46'48''.

Por otro lado, si quieres convertir un ángulo en grados sexagesimales, por ejemplo de 45º46'48'', expresado en grados, minutos y segundos a su forma decirmal (es decir, expresado únicamente en grados, sin submúltplos):

• Pasamos los segundos a minutos, dividiendo entre 60. En nuestro ejemplo dividimos 48'' entre 60, quedando 48/60=0.8'
• Sumamos los minutos que tenemos con los minutos obtenidos al pasar segundos a minutos, en el punto anterior. En nuestro ejemplo, 46'+0.8'=46.8'
• Pasamos los minutos a grados, dividiendo entre 60. En nuestro ejemplo dividimos 46.8' entre 60, quedando 46.8/60=0.78º
• Sumamos los grados que tenemos con los grados obtenidos al pasar los minutos a grados, en el punto anterior. En nuestro ejemplo, 45º+0.78º=45.78º

Por tanto, como ya sabíamos 45º46'48''=45.78º

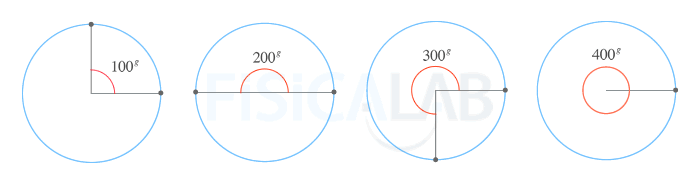
Sistema centesimal

De forma similar al sistema sexagesimal, el ángulo completo se divide en determinadas partes denominadas grados centesimales (1^g), aunque en esta ocasión dicha división se realiza en 400 partes iguales. Cada grado centesimal, también llamado gon, gonio o gradián, se divide en 100 minutos centesimales (100^m) y cada minuto se divide en 100 segundos centesimales (100^s).

1^g = 100^m
1^m = 100^s

Principales ángulos en grados centesimales

Como puedes observar, en el sistema centesimal el ángulo recto corresponde a 100^g y el llano a 200^g.

Cálculo en radianes

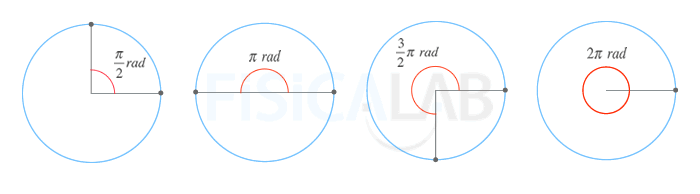
Al igual que los grados sexagesimales o centesimales existe otra unidad denominada radián (rad) cuya principal diferencia es que relaciona el ángulo que representa con la longitud del arco recorrido al girarlo. El radián es la unidad de ángulos en el Sistema Internacional de unidades.

Radián

Un radián es la porción de plano limitada por un arco de circunferencia igual a su radio.

Si tenemos en cuenta que la longitud de una circunferencia es 2·π·r se cumple que un ángulo completo en radianes es:

Principales ángulos en radianes

En el Sistema Internacional el ángulo recto corresponde a π/2 rad y el llano a π.

Transformación entre grados sexagesimales y radianes

Grados sexagesimales a radianes

Para transformar cualquier ángulo expresado en grados sexagesimales (Ej. 10º 12' 24'') a radianes, en primer lugar, vamos a convertirlo completamente a grados (con decimales) y posteriormente a radianes:

1. Convertiremos los grados, minutos y segundos a un valor expresado únicamente en grados (si ya no lo está). Para ello:
   1. Multiplica los minutos (') por 1º/60'. Ej. 12' = 12' · 1º/60' = 0.2º
   2. Multiplica los segundos ('') por 1º/3600''. Ej 24" = 24" · 1º/3600" = 0.007º
   3. Súma los dos resultados anteriores a los grados del ángulo y ese será el mismo ángulo expresado únicamente en grados . Ej. 10º 12' 24'' = 10º+0.2º+0.007º = 10.207º 
2. El ángulo en radianes se obtiene al multiplicar por π/180 los grados calculados anteriormente. Ej.  10.207º = 10.207º · π rad/180º = 0.178 rad

Radianes a Grados Sexagesimales

Para transformar cualquier ángulo en grados sexagesimales ( Ej. 2.23 rad ) en primer lugar lo convertiremos completamente a grados (con decimales) y posteriormente a grados, minutos y segundos.

1. Multiplica los radianes por 180/π. De esta forma obtenemos los grados. Ej. 2.23 rad = 2.23 rad · 180º/π rad = 127.7695º
2. Si obtenemos decimales, los multiplicamos por 60'/1º. Ej 0.7695º · 60'/1º = 46.17'
3. Si obtenemos nuevamente decimales los multiplicamos por 60"/1'. Ej 0.17' · 60"/1 = 10.2"
4. La parte entera de cada uno de llos resultados obtenidos en los paso 1, 2 y 3 es el ángulo sexagesimal: Ej. 127º 46' 10"

Reducción de un ángulo al primer giro

Imagina un coche dando vueltas en una pista circular. Tras varias vueltas el ángulo que se habrá desplazado será mayor que la de un ángulo completo: 360º = 2 π rad, aunque al final el ángulo de su posición se pueda determinar únicamente con el ángulo de su última vuelta (entre 0º y 360º). Por esta razón:

Reducir grados sexagesimales al primer giro

1. Si el ángulo es mayor que 360º, el ángulo reducido al primer giro es el resto de la división del ángulo entre 360º
2. Si el ángulo es menor que 0º, dividimos como en el caso anterior, pero considerando el ángulo positivo. El resto obtenido lo restamos a 360º

Reducir radianes al primer giro

1. Si el ángulo es mayor que 2π rad, el ángulo es el resto de la división entre el ángulo y 2π rad
2. Si el ángulo es menor que 0 rad, dividimos como en el caso anterior, pero considerando el ángulo positivo. El resto obtenido lo restamos a 2π rad

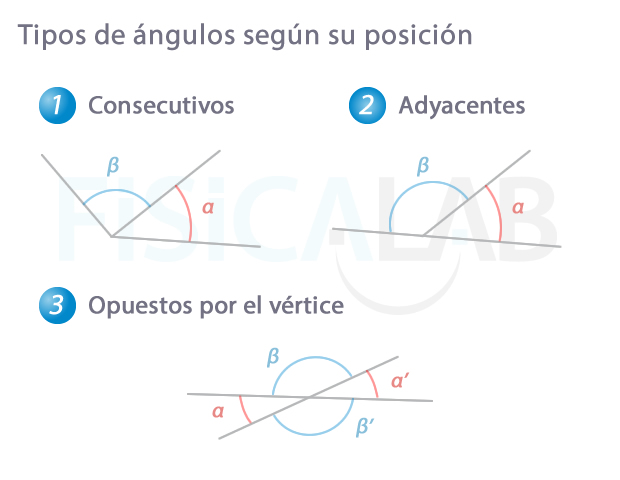
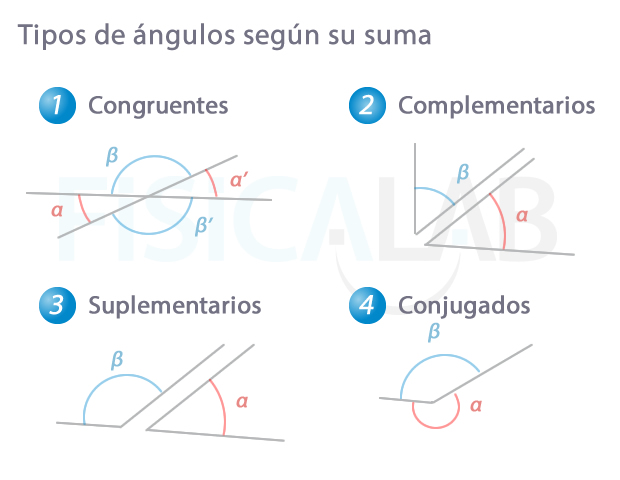
Tipos de ángulos

Existen distintas clasificaciones posibles para los ángulos. Veamos algunas.

Tipos de ángulos según su amplitud

El transportador de ángulos en la parte inferior central de la figura, es una herramienta usada para medir ángulos. Estos se pueden clasificar, según su amplitud en:

• Ángulo nulo: Es decir, de 0º o 0 rad
• Ángulo recto: Es un ángulo de 90º o π/2 rad
• Ángulo llano: Es un ángulo de 180º o π rad

Por otro lado:

• Ángulos agudos: Son aquellos entre 0º y 90º, o 0 rad y π/2 rad
• Ángulos obtusos: Son aquellos entre 90º y 180º, o π/2 rad y π rad

Finalmente, recuerda que llamamos ángulo completo o perigonal al de 360º o 2π.

Por otro lado, a los ángulos que no son rectos ni múltiplos de uno recto se le llaman ángulos oblicuos. Por ejemplo, los ángulos de 35º o de 2 rad son ángulos oblicuos.

Ángulos cócavos y convexos

Dadas dos semirectas que parten de un origen común, siempre quedan determinados dos ángulos: Al de menor amplitud lo denominamos convexo (en rojo). Al de mayor amplitud lo denominamos cóncavo (en azul).

Tipos de ángulos según su posición

Atendiendo a su posición, los ángulos pueden clasificarse en:

1. Ángulos consecutivos: Son aquellos que comparten el vértice y un lado
2. Ángulos adyacentes: Aquellos que, compartiendo el vértice y un lado, tienen sus otros dos lados como semirrectas opuestas. Observa que, según esta definición, dos ángulos adyacentes son a la vez consecutivos y suplementarios, según la definición que veremos más abajo, y por ello suman 180º
3. Ángulos opuestos por el vértice: Cuando los lados de uno son semirrectas opuestas a los lados del otro . En la figura α y α' son opuestos por el vértice. Por otro lado, β y β' también lo son

Tipos de ángulos según la suma de sus amplitudes

Según la suma de sus amplitudes, dos ángulos pueden ser:

• Congruentes: Tienen la misma amplitud
• Complementarios: Suman 90º
• Suplementarios: Sus amplitudes suman 180º. Observa que dos ángulos adyacentes, según la definición anterior son sumplementarios
• Conjugados u opuestos: Suman 360º