Razones Trigonométricas de Ángulos Agudos

La trigonometría es el estudio de los triángulos, estos es, de las relaciones entre los ángulos y los lados que los componen. En este apartado vamos a estudiar las razones trigonométricas de ángulos agudos (menores de 90º o π/2 rad) a través de los siguientes puntos:

• Razones del triángulo rectángulo
  • Seno
  • Coseno
  • Tangente
  • Cosecante
  • Secante
  • Cotangente
• Propiedades de las razones trigonométricas
  • Identidad fundamental de la trigonometría
• Uso de la calculadora

Si ya estás familiarizado con estas ideas, te recomendamos que visites el apartado sobre las razones trigonométricas de cualquier ángulo.

¿Empezemos?

Razones trigonométricas en un triángulo rectángulo

A partir de cualquier ángulo agudo α (menor de 90º) es posible construir un triángulo rectángulo ABC como el que puedes apreciar en la siguiente figura.

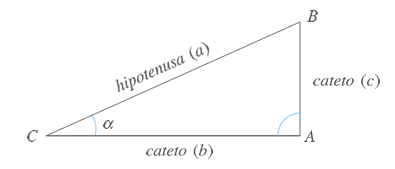
Triángulo rectángulo

Cualquier triángulo rectángulo posee dos ángulos agudos y uno recto.

Teniendo en cuenta dicha figura geométrica y los ángulos formados en cada uno de sus vértices es posible obtener una serie de razones que reciben el nombre de razones trigonométricas conocidas como seno, coseno, tangente, cosecante y cotangente.

Seno

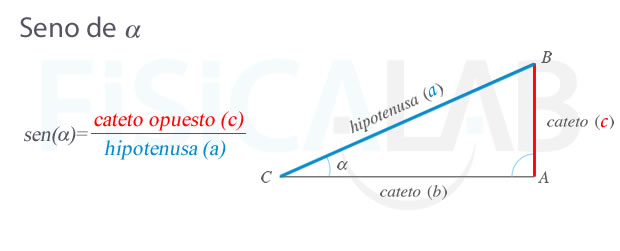
Definición de seno de un ángulo

Podemos encontrar el valor del seno de un ángulo dividiendo el cateto opuesto a dicho ángulo entre la hipotenusa del triángulo rectángulo. Ten presente que el cateto opuesto es aquel que está "frente" al ángulo (no "toca" el ángulo).

Coseno

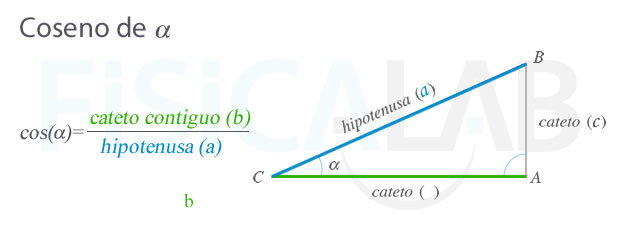
Definición de coseno de un ángulo

Podemos encontrar el valor del coseno de un ángulo dividiendo el cateto contiguo a dicho ángulo entre la hipotenusa del triángulo rectángulo. Ten presente que el cateto contigo es aquel que está "adyacente" al ángulo (toca al ángulo por uno de sus extremos). Recuerda, como regla mnemotécnica, "coseno=contiguo".

Tangente

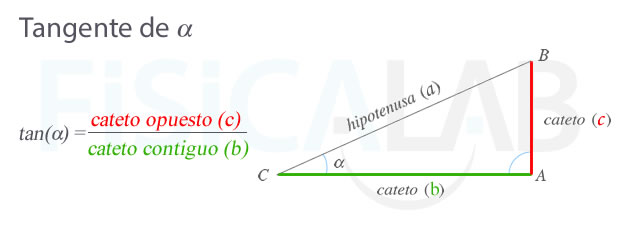
Definición de tangente de un ángulo

Podemos encontrar el valor de la tangente de un ángulo dividiendo el seno entre el coseno de dicho ángulo o, dicho de otra manera, dividiendo el cateto opuesto entre el contiguo a dicho ángulo.

Demostración

De las definiciones anteriores es posible deducir que:

Demostración:

$$\tan \left(\alpha \right)=\frac{\sin \left(\alpha \right)}{\cos \left(\alpha \right)}=\left\{\begin{array}{c}\\ \begin{array}{c}\sin \left(\alpha \right)=\frac{c}{a}\\ \cos \left(\alpha \right)=\frac{b}{a}\end{array}\end{array}\right\}=\frac{{\displaystyle \frac{c}{a}}}{{\displaystyle \frac{b}{a}}}=\frac{c·\cancel{a}}{b·\cancel{a}}=\frac{c}{b}$$

Cosecante

Secante

Cotangente

Propiedades de las razones trigonométricas

Dado que se trata de un ángulo agudo ( 0 < α < 90º ) podemos deducir que:

¿Sabrías decir por qué? Efectivamente, dado que en el seno y en el coseno se divide entre la hipotenusa, y este es el lado mayor, siempre mayor que los catetos, el cociente será siempre menor que 1.

Identidad fundamental de la trigonometría

A partir del teorema de Pitágoras podemos deducir lo que se conoce como identidad pitagórica:

Demostración:

$${\sin }^2\left(\alpha \right)+{\cos }^2\left(\alpha \right)={\left(\frac{c}{a}\right)}^2+{\left(\frac{b}{a}\right)}^2=\frac{c^2+b^2}{a^2}=\left\{a^2=b^2+c^2\right\}=\frac{a^2}{a^2}=1$$

Si dividimos la identidad pitagórica por cos²(α) obtenemos que:

Demostración:

$$\begin{gathered} \frac{{\sin }^2\left(\alpha \right)}{{\cos }^2\left(\alpha \right)}+\frac{\cancel{{\cos }^2\left(\alpha \right)}}{\cancel{{\cos }^2\left(\alpha \right)}}=\frac{1}{{\cos }^2\left(\alpha \right)}; \\ {\left(\frac{\sin \left(\alpha \right)}{\cos \left(\alpha \right)}\right)}^2+1={\left(\frac{1}{\cos \left(\alpha \right)}\right)}^2; \\ {\tan }^2\left(\alpha \right)+1={\sec }^2\left(\alpha \right) \end{gathered}$$

Por otro lado, si dividimos la identidad pitagórica por sin²(α) obtenemos que:

Demostración:

$$\begin{gathered} \frac{\cancel{{\sin }^2\left(\alpha \right)}}{\cancel{{\sin }^2\left(\alpha \right)}}+\frac{{\displaystyle {\cos }^2}\left(\alpha \right)}{{\sin }^2\left(\alpha \right)}=\frac{1}{{\displaystyle {\sin }^2}\left(\alpha \right)}; \\ 1+{\left(\frac{{\displaystyle \cos \left(\alpha \right)}}{\sin \left(\alpha \right)}\right)}^2={\left(\frac{1}{\sin \left(\alpha \right)}\right)}^2 ; \\ 1+{\cot }^2\left(\alpha \right) ={\csc }^2\left(\alpha \right) \end{gathered}$$

Calculadora

Podemos calcular las razones trigonométricas de cualquier ángulo agudo (y de cualquier ángulo, en general) con nuestra calculadora. Tenemos para ello las teclas:

• : Para el cálculo del seno. La palabra sin es del inglés sinus (seno), aunque en algunas calculadoras tienes directamente sen
• : Para el cálculo del coseno
• : Para el cálculo de la tangente

Es muy importante que sepas como la calculadora va a interpretar el ángulo que estás poniendo. Así, si tienes tu calculadora configurada en grados sexagesimales probablemente verás en la línea superior y en pequeñito la letra D (del inglés degree). Significa que cuando pongas, por ejemplo sin(30), la calculadora resolverá sin(30º)=0.5. En cambio, si tienes tu calculadora configurada en radianes (apareciendo en la línea superior y en pequeñito la letra R de radianes), y pones sin(30) la calculadora resolverá sin(30 rad)=-0.988.