Movimiento Armónico Simple en Péndulos

El péndulo simple se puede considerar un caso de movimiento armónico simple (m.a.s.), cuando se cumplen ciertas condiciones que veremos en este apartado. Aprenderemos:

• Qué es un péndulo simple
• Las fuerzas que intervienen en el movimiento del péndulo
• Bajo qué condiciones se puede considerar el péndulo un m.a.s.
• De qué depende el periodo del péndulo

También puedes:

• Tener una visión general sobre el movimiento armónico simple y sus magnitudes

Concepto de péndulo simple

Nos interesa conocer si podemos aplicar los conceptos propios del m.a.s. al estudio del péndulo. Recuerda que una partícula o sistema tiene movimiento armónico simple (m.a.s) cuando oscila bajo la acción de fuerzas restauradoras que son proporcionales a la distancia respecto a la posición de equilibrio.

¿Cómo se comportan los péndulos?

Cuando el péndulo se encuentra en reposo, en vertical, permanece en equilibrio ya que la fuerza peso es contrarrestada por la tensión en la cuerda.

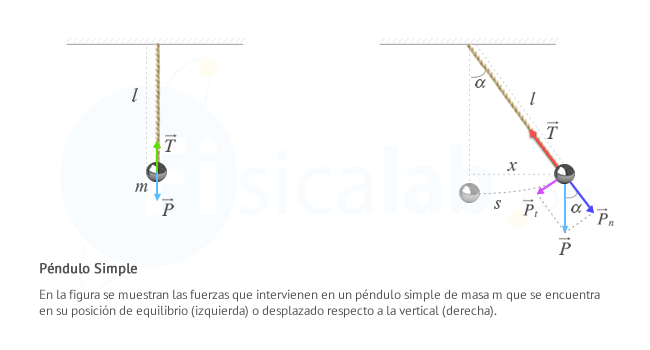
Cuando se separa de la posición de equilibrio la tensión contrarresta solo a la componente normal del peso, siendo la componente tangencial del peso la fuerza resultante. Esta fuerza es la responsable de que aparezca una aceleración ( F = m · a ) que trata de devolver al péndulo a su posición de equilibrio.

$${\overrightarrow{P}}_n+\overrightarrow{T}\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em}; P_t=-m·g·\sin \left(\alpha \right)$$

Componentes tangencial y normal de una fuerza

Es posible que no recuerdes con claridad qué es la componente tangencial y normal de una fuerza, también llamadas componentes intrínsecas. Para definirlas utilizamos un sistema de referencia intrínseco en cada punto de la trayectoria, tal y como se puede ver en la figura.

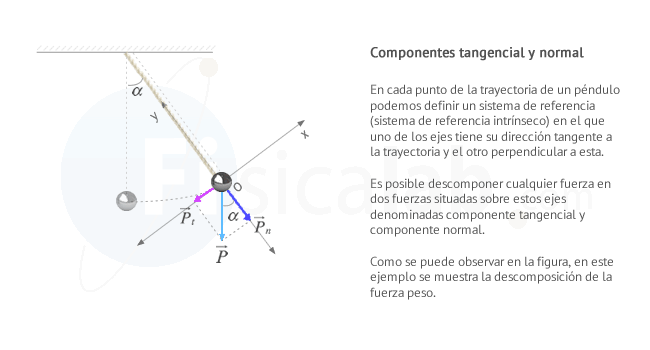
Es importante que Observes que el sistema de referencia se establece para cada punto de la trayectoria: Uno de los ejes es tangente a la trayectoria en ese punto. El otro es perpendicular al primero, es decir, normal a la trayectoria en ese punto.

Una vez establecidos los ejes en cada punto de la trayectoria podemos descomponer las fuerzas en estos ejes:

• Componente tangencial: Es la proyección de la fuerza sobre el eje tangente
• Componente normal: Es la proyección de la fuerza sobre el eje normal

El péndulo simple como oscilador armónico

Comprobación

Un oscilador armónico no es más que una partícula que se mueve según un m.a.s. La aceleración que aparece en el péndulo cuando se separa de su posición de equilibrio hace que el péndulo vibre u oscile en torno a su posición de equilibrio. Dichas vibraciones siguen el patrón de un movimiento armónico simple si el ángulo de oscilación es pequeño (no más de 15º o 20º). Esto implica que:

1. $\sin \left(\alpha \right)\cong \alpha$ 
2. La longitud de la trayectoria curva s y el desplazamiento x en el eje horizontal tienden a igualarse
3. La aceleración normal es despreciable
4. Se puede considerar que la trayectoria del móvil es horizontal
5. La posición viene dada por la separación x a la vértical de equilibrio

Con lo anterior nos queda:

$$P_t=-m·g·\sin \left(\alpha \right)\cong -m·g·\alpha \underset{s=l·\alpha }{=}-m·g·\frac{s}{l}\cong -m·g·\frac{x}{l}=m·a$$ 

Con lo que podemos afirmar que la aceleración es proporcional al desplazamiento pero de sentido contrario, siendo

$$a=-\frac{g}{l}·x$$

Periodo del péndulo simple

El periodo del péndulo simple, para oscilaciones de poca amplitud, viene determinado por la longitud del mismo y la gravedad. No influye la masa del cuerpo que oscila ni la amplitud de la oscilación.

¿Cómo determinar el valor de la gravedad con un péndulo?

La expresión anterior nos permite calcular el periodo conocidas la longitud del péndulo y el valor de la gravedad. Siguiendo el proceso inverso podemos determinar el valor de la gravedad. Conocida la longitud l, medimos el tiempo que tarda el péndulo en realizar una oscilación completa y aplicamos la siguiente expresión, despejada de la expresión del periodo anterior:

$$g={\left(\frac{2·\pi }{T}\right)}^2·l {\text{m/s}}^2$$ 

Para ver un desarrollo de la obtención de la anterior expresión, visita el apartado de dinámica del movimiento armónico simple.