Estudio Energético del Movimiento Armónico Simple

Para estudiar las componentes energéticas del movimiento armónico simple podemos suponer que no hay fuerzas de fricción o rozamiento (fuerzas no conservativas) y por tanto la energía mecánica, compuesta principalmente de energía cinética y energía potencial elástica, permanece constante. En este apartado veremos:

• La energía cinética del m.a.s. y sus gráficas
• La energía potencial del m.a.s. y sus gráficas
• La energía mecánica del m.a.s. y sus gráficas
• La relación que guardan entre sí las componentes anteriores

Energía cinética en el m.a.s.

La energía cinética en un movimiento armónico simple en un punto está asociada a la velocidad que el cuerpo tiene en dicho punto. Recuerda que la velocidad en un oscilador armónico es máxima en la posición de equilibrio y 0 en los extremos.

El valor máximo de la energía cinética es $E_c=\frac{1}{2}·k·A^2$  y el valor mínimo es 0.

Gráficas de la energía cinética en m.a.s.

Existen dos tipos de gráficas posibles para la energía cinética de un oscilador armónico: las que relaciónan la energía cinética con la elongación y las que la relacionan con el tiempo

Gráfica energía cinética - posición

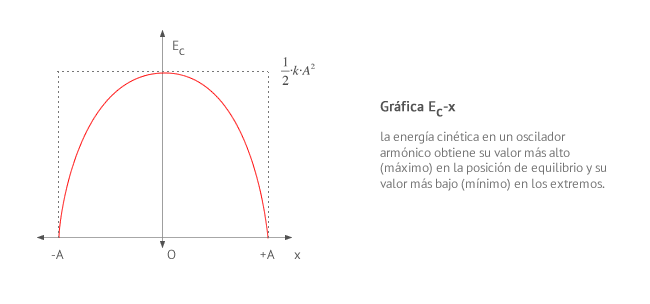
Gráficas energía cinética - tiempo

Comprobación

La energía cinética de un cuerpo viene dada por la expresión:

La velocidad en el movimiento armónico simple viene dada en función del tiempo por la expresión:

Sustituyendo la segunda en la primera expresión, nos queda:

$$\begin{gathered} E_c=\frac{1}{2}·m·v^2=\frac{1}{2}·m·{\left(-A·\omega ·\sin \left(\omega ·t+{\phi }_0\right)\right)}^2\underset{1}{=}\frac{1}{2}·k·A^2·{\sin }^2\left(\omega ·t+{\phi }_0\right) \\ 1. k=m·{\omega }^2 \end{gathered}$$

Por otro lado, la velocidad en el movimiento armónico simple viene dada en función de la elongación por la expresión

Sustituyendo esta en la primera expresión, nos queda:

$$\begin{gathered} E_c=\frac{1}{2}·m·v^2=\frac{1}{2}·m·{\left(\pm \omega ·\sqrt{A^2-x^2}\right)}^2\underset{1}{=}\frac{1}{2}·k·\left(A^2-x^2\right) \\ 1. k=m·{\omega }^2 \end{gathered}$$

Observa que, implicitamente, hemos considerado la expresión de la elongación x en función del coseno, ya que la velocidad v aparece en función del seno. Es por ello que la expresión de la energía cinética en función del tiempo queda en forma de seno. Si hubiésemos eligido el seno como expresión de la elongación x llegaríamos a una expresión de la energía cinética complementaria, en función del coseno. En cualquiera de los casos, cuando resuelves un problema concreto, los resultados deben ser iguales independientemente de la expresión que elijas: no olvides la fase inicial ${\phi }_0$ .

Energía potencial en el m.a.s.

La fuerza recuperadora o elástica es una fuerza conservativa. El trabajo realizado por las fuerzas conservativas depende unicamente de los puntos inicial y final, y no del camino elegido. Por ello, las fuerzas conservativas dan lugar a la energía potencial. En este caso se trata de energía potencial elástica, al ser la fuerza responsable la fuerza recuperadora o elástica.

El valor máximo de la energía potencial es $E_c=\frac{1}{2}·k·A^2$  y el valor mínimo es 0.

Gráficas de la energía potencial en m.a.s.

Existen dos tipos de gráficas posibles para la energía potencial de un oscilador armónico: las que relaciónan la energía potencial con la elongación y las que la relacionan con el tiempo

Gráfica energía potencial - posición

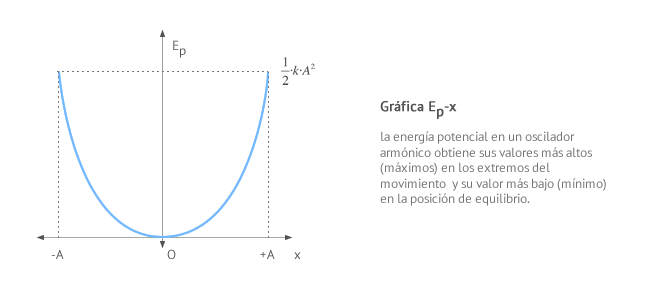
Gráficas energía potencial - tiempo

Comprobación

El trabajo que realiza la fuerza recuperadora $\overrightarrow{F}=-k·\overrightarrow{x}$ para ir de un punto inicial A a otro final B viene dado por: 

$$W_{A\to B}={\int }_A^B\overrightarrow{F}·d\overrightarrow{r}={\int }_{x_A}^{x_B}-k·x·dx={\left[-\frac{1}{2}·k·x^2\right]}_{x_A}^{x_B}=\frac{1}{2}·k·{x_A}^2-\frac{1}{2}·k·{x_B}^2$$

Por otro lado, sabemos que la fuerza elástica es una fuerza conservativa. El trabajo realizado por una fuerza conservativa puede expresarse en función de la diferencia de energía potencial:

$$W_{A\to B}=-∆E_p=-(E_{p_B}-E_{p_A})=E_{p_A}-E_{p_B}$$

Comparando las dos expresiones anteriores podemos deducir que:

$$\begin{array}{c}{E}_{p_A}=\frac{1}{2}·k·{x_A}^2\\ E_{p_B}=\frac{1}{2}·k·{x_B}^2\end{array}$$

Con esto podemos escribir la energía potencial en función de la elongación, esto es, en cualquier punto x como:

$$E_p=\frac{1}{2}·k·x^2$$

Por otro lado la elongación en un movimiento armónico simple viene determinada por:

Sustituyendo en la expresión de la energía potencial, obtenemos la expresión de la energía potencial en el m.a.s. en función del tiempo:

$$E_c=\frac{1}{2}·k·A^2·{\cos }^2\left(\omega ·t+{\phi }_0\right)$$ 

Observa que hemos considerado la expresión de la elongación x en función del coseno. Es por ello que la expresión de la energía potencial en función del tiempo queda en forma de coseno. Si hubiésemos elegido el seno como expresión de la elongación x llegaríamos a una expresión de la energía potencial complementaria, en función del seno. En cualquiera de los casos, cuando resuelves un problema concreto, los resultados deben ser iguales independientemente de la expresión que elijas: no olvides la fase inicial ${\phi }_0$ .

Energía mecánica en el m.a.s

La energía mecánica de un oscilador armónico en un punto es la suma de la energía cinética y la energía potencial en dicho punto.

¿De qué depende la energía mecánica en el m.a.s.?

A partir de la expresión anterior, podemos decir que la energía mecánica es directamente proporcional a la amplitud A del movimiento, a su frecuencia f y a la masa m del cuerpo que oscila:

$$E_m=\frac{1}{2}·k·A^2=\frac{1}{2}·m·{\omega }^2·A^2=\frac{1}{2}·m·4·{\pi }^2·f^2·A^2$$ 

Gráficas de la energía mecánica en el m.a.s

La energía mecánica es constante en el m.a.s. en cualquier punto y en cualquier instante de tiempo. Por tanto sus gráficas son las siguientes.

Gráfica energía mecánica - posición

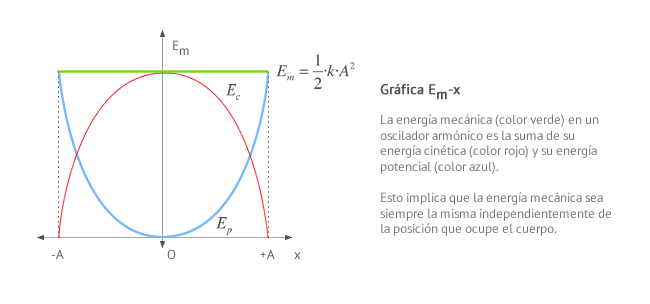
Gráficas energía mecánica - tiempo

Comprobación

Si sustituimos las expresiones de la energía cinética y la energía potencial en la expresión de la mecánica, obtenemos el resultado buscado:

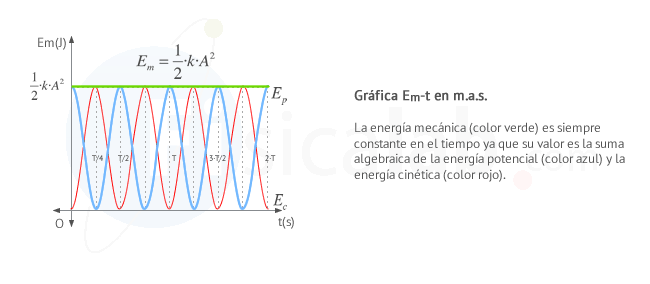
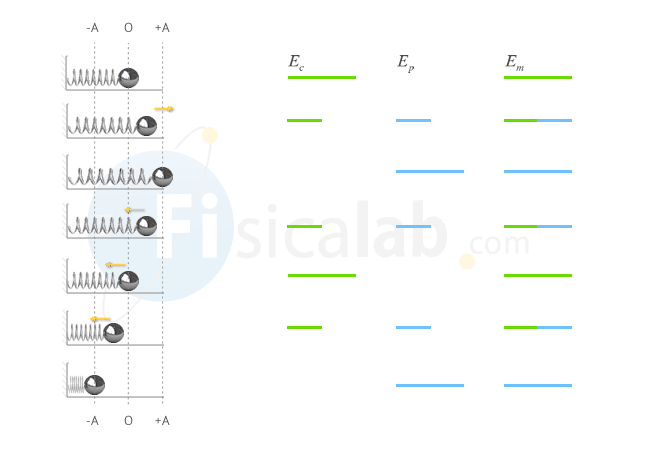
Relación entre energía cinética, potencial y mecánica en el m.a.s.

La suma de la energía cinética y la potencial en un movimiento armónico simple siempre es constante en cualquier instante de tiempo y en cualquier posición del cuerpo.