Movimiento Armónico Simple en Muelles

Los muelles están presentes en una gran y variada cantidad de objetos que te rodean: colchones, pesos, automóviles, bicicletas. En este apartado veremos:

• Si los muelles son considerados osciladores armónicos
• Qué ocurre cuando cuelgas un cuerpo de un muelle vertical

¿Son los muelles osciladores armónicos?

Un oscilador armónico es cualquier partícula o sistema que se mueve según un movimiento armónico simple.

Comprobación en cuerpo suspendido por muelle

En un oscilador armónico existe una posición de equilibrio estático. Cuando la partícula se separa de dicha posición de equilibrio aparece una fuerza proporcional a la distancia de separación. Para comprobar si un muelle se comporta como un oscilador armónico podemos distinguir dos casos típicos:

1. Muelle vertical desde el que se cuelga un cuerpo. En él intervienen dos fuerzas, la fuerza elástica F_e , que sigue la ley de Hooke, y el peso P 
2. Muelle horizontal unido a un cuerpo. En este caso sólo interviene una fuerza, la fuerza elástica F_e

Dado que el segundo caso es una simplificación del primero en el que la fuerza total es directamente F_e, vamos a comprobar que, en el primero de los casos, el cuerpo efectivamente se comporta como un oscilador armónico. 

Partimos de un muelle de constante elástica k, cuya posición de equilibrio es L₀, desde el que cuelga una partícula de masa m. Al colgar la partícula, la posición de equilibrio pasa a ser l₀ = L₀ + x₀. Recuerda que la fuerza elástica en un muelle sigue la ley de Hooke.

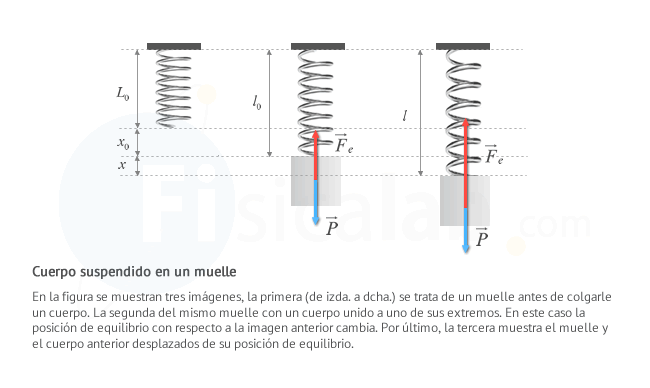
1. En equilibrio

   • La partícula unida al muelle no tiene aceleración. Por tanto, la fuerza resultante que actúa sobre la partícula ${\overrightarrow{F}}_t=0$ 

     $${\overrightarrow{F}}_t={\overrightarrow{F}}_e+\overrightarrow{P}=-k·{\overrightarrow{x}}_0+m·\overrightarrow{g}=0\Rightarrow k·x_0=m·g$$

2. Si tiras del muelle hacia abajo y sueltas
   • La fuerza elástica crece de manera proporcional a la distancia de separación a la posición de equilibrio. $F_e=-k·(x_0+x)$ . Observa que al crecer, su valor ahora será mayor que el del peso

   • Por ello, la fuerza resultante ${\overrightarrow{F}}_t={\overrightarrow{F}}_e+\overrightarrow{P}\ne 0$  ,lo que hace que aparezca una aceleración que trata de devolver al muelle a su posición original de equilibrio

     Considerando el sentido positivo hacia abajo y que, tal y como habíamos visto, $k·x_0=m·g$ ,nos queda:

     $$F_t=-k(x_0+x)+m·g=-k·x_0-k·x+m·g=-\cancel{m·g}-k·x+\cancel{m·g}=-k·x$$

     Observa la similitud que tiene la expresión $F_t=-k·x$  con la ley de Hooke, pero ten en cuenta que x es la distancia a la posición que tiene el cuerpo cuando se cuelga del muelle y no, directamente, a la posición de equilibrio del propio muelle sin objeto colgado L₀ .

     La fuerza total que actúa sobre un objeto cuando cuelga de un muelle tiene igual valor que la fuerza elástica de un hipotético muelle cuya posición de equilibrio fuese L₀ + x₀ y por tanto x su distancia a la posición de equilibrio. 

     Teniendo en cuenta el principio fundamental o Segunda Ley de Newton, podemos calcular la aceleración del cuerpo en cada punto de su oscilación:

     $$F_t=m·a\Rightarrow -k·x=m·a\Rightarrow a=-\frac{k}{m}·x$$

3. Cuando el muelle vuelve a pasar por la posición de equilibrio x₀ lo hace con cierta velocidad. Una vez cruzada dicha posición la aceleración que actúa sobre la partícula cambia de sentido haciendo que la velocidad disminuya su módulo hasta detenerse en el extremo contrario al punto en que se inició el movimiento.
4. El proceso se repite como si nos encontráramos de nuevo en el punto 2. Ten en cuenta que si no existiese rozamiento, el muelle nunca pararía.

En el siguiente experimenta y aprende tienes un muelle. Estíralo o comprímelo y súeltalo para observar como la partícula sigue un movimiento armónico simple. Concretamente, la distancia a la posición de equilibrio varía en forma de sinusoide con el paso del tiempo.