Aceleración Centrípeta o Normal
En Física decimos que un cuerpo tiene aceleración cuando se produce un cambio del vector velocidad, ya sea en módulo o dirección. En apartados anteriores hemos visto que la aceleración se puede clasificar según el efecto que produce en la velocidad en aceleración tangencial (si hace que cambie el módulo del vector velocidad) y aceleración normal o centrípeta (si hace que cambie su dirección). Son las componentes intrínsecas de la aceleración. En este apartado vamos a desarrollar con mayor profundidad la aceleración centrípeta o normal.
Aceleración centrípeta o normal
La aceleración normal o centrípeta mide los cambios de dirección de la velocidad en el tiempo. Su expresión viene dada por:
Donde:
La aceleración normal puede ser:
- =0: En los movimientos rectilíneos, donde la dirección permanece constante
- >0: En los movimientos curvilíneos, donde la velocidad cambia continuamente de dirección
Observa que cualquier trayectoria que describa un cuerpo se puede considerar como una composición de trayectorias rectas y curvas. Las partes curvas de la trayectoria pueden a su vez considerarse arcos de circunferencia. La siguiente imagen ilustra este concepto
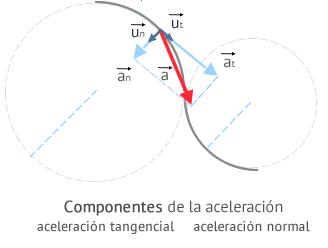
Como vemos, el centro de curvatura de un punto de la trayectoria curva es el centro de la circunferencia que pasa por él. El radio de dicha circunferencia es el radio de curvatura de dicho punto.
Demostración de la aceleración normal
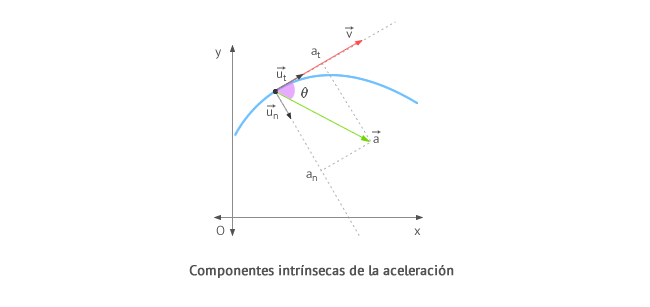
Con anterioridad hemos visto que la aceleración instantánea es la derivada de la velocidad respecto al tiempo. Por otro lado, hemos visto que podemos expresar el vector velocidad como el producto de su módulo por un vector unitario tangente a la trayectoria:
Donde hemos aplicado la regla de derivación de un producto D(ab)=a'b+ab'.
Vemos que el segundo término es el producto del módulo de la velocidad por la derivada de
-
Expresamos
-
Aplicamos la regla de la cadena
-
De lo anterior se deduce:
El término encuadrado corresponde a la aceleración centrípeta o normal y es la responsable de que la velocidad cambie su dirección a lo largo del tiempo.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:
