Fuerzas en el Movimiento Armónico Simple

La fuerza total que actúa sobre una partícula en un movimiento armónico simple es proporcional a la distancia a la posición de equilibrio. En este apartado vamos a ahondar en el estudio de las fuerzas presentes en el m.a.s. Para ello estudiaremos:

• El comportamiento dinámico del oscilador armónico
• Las fuerzas que aparecen en un muelle
• Las fuerzas que aparecen en un péndulo

Adicionalmente, puede que te interese profundizar en:

• El concepto de movimiento armónico simple u oscilador armónico
• Sus gráficas y ecuaciones a través del estudio de la cinemática del movimiento armónico simple

No olvides que la fuerza es, en general, una magnitud vectorial. Sin embargo, en este apartado, dado que el m.a.s. se desarrolla en una sola dimensión, podremos utilizar el convenio de signos en movimientos rectilíneos habitual.  

Comportamiento dinámico del m.a.s.

Podemos estudiar el movimiento armónico simple (m.a.s.), desde un punto de vista dinámico, es decir, atendiendo a las fuerzas presentes en el movimiento. Recuerda que un oscilador armónico es cualquier cuerpo que se mueve según un m.a.s. Cuando estudiamos la cinemática del movimiento armónico simple, llegamos a la siguiente relación entre aceleración y posición:

Desarrollando la idea anterior, nos queda:

$$\overrightarrow{F}=m·\overrightarrow{a}=m·(-{\omega }^2·\overrightarrow{x})=-m·{\omega }^2·\overrightarrow{x}=-k·\overrightarrow{x}$$

La fórmula anterior simplemente nos indica que la fuerza presente en un movimiento armónico simple, que actúa en calidad de fuerza restauradora, trata de devolver al cuerpo a su posición de equilibrio desde el punto en el que se encuentre.

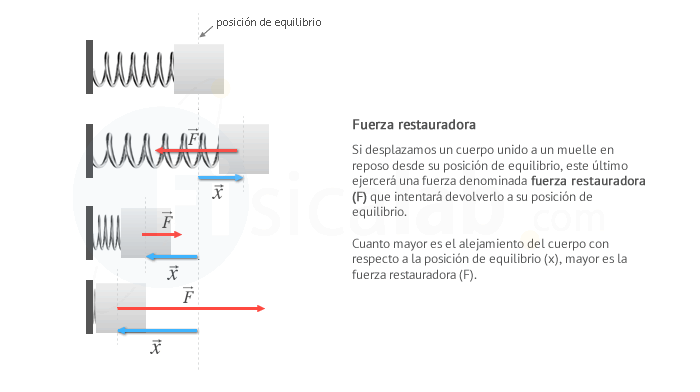
Caracterización dinámica de un oscilador armónico

Podemos caracterizar los osciladores armónicos a partir de los valores de su constante k y su masa m, dando lugar a los valores característicos de frecuencia angular ω, periodo T y frecuencia f.

Frecuencia angular ω

$$\omega =\sqrt{\frac{k}{m}} \text{rad/s}$$

Periodo T

$$T=\frac{2·\pi }{\omega }=2·\pi ·\sqrt{{\displaystyle \frac{m}{k}}} \text{s}$$

Frecuencia f

$$f=\frac{\omega }{2·\pi }=\frac{1}{2·\pi }·\sqrt{\frac{k}{m}} \text{Hz}$$

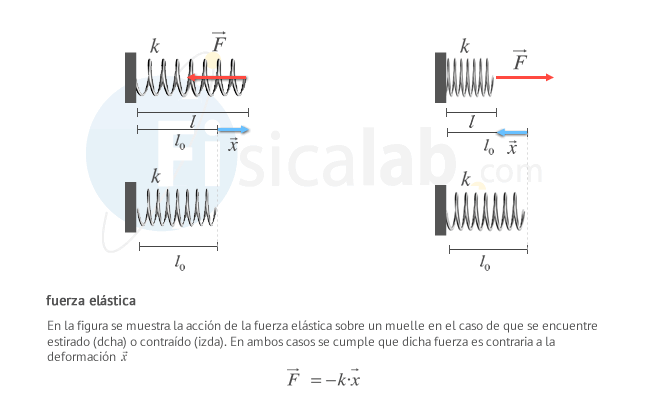
Fuerzas presentes en los muelles

Si observas la expresión de la fuerza que actúa en un m.a.s. \overrightarrow{F}=-k·\overrightarrow{x}  ,te darás cuenta que es la ley de Hooke. 

El m.a.s. en muelles ocurre por el simple hecho de encontrarse estos sometidos a una fuerza proporcional a la distancia a la posición de equilibrio y de sentido contrario. La constante de proporcionalidad, k , coincide con la constante elástica de la ley de Hooke. Esto nos permite conocer el valor de la fuerza restauradora para un determinado desplazamiento respecto a la posición de equilibrio a partir de la frecuencia angular del movimiento y la masa del cuerpo que oscila.

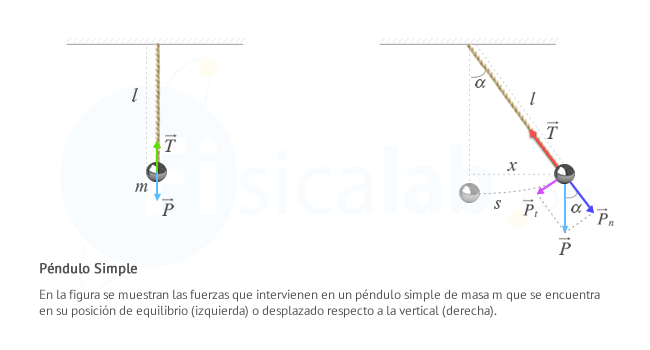
Fuerzas presentes en los péndulos

El m.a.s. en péndulos se produce cuando la amplitud es pequeña. La fuerza resultante sobre el péndulo, la componente tangencial del peso P_t , es proporcional en este caso al desplazamiento horizontal de la vertical de equilibrio. 

Comprobación

A continuación comprobamos la validez de la expresión anterior, teniendo en cuenta que, para oscilaciones pequeñas, la componente tangencial del peso P_t  se puede considerar aproximadamente horizontal y por ello la llamaremos P_x, quedando:

$$\left.\begin{array}{r}F=P_t\simeq P_x=-m·g·\sin \left(\alpha \right)=-m·g·\frac{x}{l}\\ F=-k·x\end{array}\right\}\to k=\frac{m·g}{l}$$

Sustituyendo en la expresión de la pulsación nos queda, obtenemos la ecuación buscada:

$$\left.\begin{array}{r}\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{m·{\displaystyle \frac{g}{l}}}{m}}=\sqrt{\frac{g}{l}}\\ \omega =\frac{2·\pi }{T}\end{array}\right\}\to T=2·\pi ·\sqrt{\frac{l}{g}}$$