Fuerza elástica en m.a.s. a partir de gráfica
Enunciado
La gráfica de la figura corresponde a un cuerpo de 150 g de masa que realiza un movimiento armónico simple (m.a.s.).
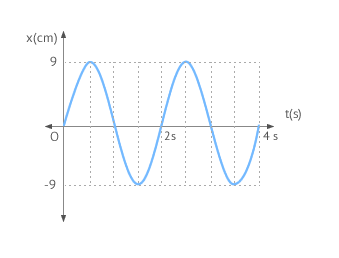
Se pide calcular:
- La velocidad inicial del cuerpo
- La aceleración en los instantes t = 2 s y t = 6 s
- El valor y sentido que tendrá la fuerza que actúa sobre el cuerpo en los instantes t = 0.5 s y t = 1.5 s
Solución
Datos
- Masa del cuerpo: m = 150 g = 0.15 kg
Consideraciones previas
A partir de las gráficas podemos sacar los siguientes valores:
- Amplitud del cuerpo: A = 9 cm = 9·10-2 m
- Periodo: T = 2 s
Resolución
1.
Recuerda que la velocidad es la derivada elongación:
Para determinar la expresión de la elongación podemos usar un seno o un coseno. En nuestro problema, por la similitud de la gráfica con la función seno, usaremos esta última.
La frecuencia angular viene dada por:
En cuanto a la fase inicial
Con todo lo anterior, ya tenemos la expresión general de la elongación:
La velocidad se calcula haciendo t = 0 s en la expresión anterior, quedando
Este valor es, además, el valor máxima de la velocidad y corresponde a la velocidad que tiene el cuerpo cuando pasa por su posición de equilibrio ( x = 0). Por ello también podríamos haber usado la expresión siguiente, con los valores adecuados.
2.
Podemos obtener la expresión de la aceleración derivando la velocidad respecto al tiempo:
Sustituyendo en los instantes señalados, nos queda:
Los resultados anteriores nos muestran que, en valores múltiplos del periodo fundamental del movimiento ( t = 2 = 2·1 s, t = 6 = 2·3 s ), el cuerpo pasa por la posición de equilibrio ( x = 0 ) resultando la aceleración ( y la fuerza elástica ) nula. Por otro lado, también podríamos usar para el cálculo la relación entre la elongación y la aceleración sabiendo que la elongación es nula en t = 2 s y t = 6 s:
3.
Finalmente, para el cálculo de la fuerza calculamos previamente la constante del movimiento armónico simple:
La fuerza elástica viene determinada por
Donde el signo menos simplemente indica que la fuerza tiene sentido contraio a la elongación
Por tanto, para
- t = 0.5 s, x = +9 =>
- t = 1.5 s, x = -9 =>
No olvides que la fuerza es una magnitud vectorial. Dado que en el m.a.s. todo el movimiento se desarrolla en una dimensión podemos usar escalares en los que los signos indican sentido. De esta forma el signo - de los valores anteriores indica que la fuerza es contraria a la elongación x
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
