Atenuación y Absorción en el Movimiento Ondulatorio

Si tiras una canica en un recipiente amplio con agua en calma podrás comprobar como los frentes de onda se van haciendo más pequeños a medida que nos alejamos del foco. Este fenómeno, denominado amortiguación, se debe fundamentalmente a dos causas:

• A la atenuación, que es debida a la forma en que se distribuye la energía en los frentes de onda
• A la absorción o disipación de energía que realiza el propio medio

En este apartado vamos a estudiar ambos.

Atenuación

Atenuación en el agua

La línea azul de la figura representa el perfil de la onda generada en un recipiente con agua. A medida que nos alejamos del foco, la energía se reparte en frentes de onda cada vez mayores, haciendo que la amplitud de la onda disminuya, como se pone de manifiesto en la línea roja, que representa la elongación máxima de la onda en cada punto.

Observa que en las ondas unidimensionales no existe atenuación ya que toda la energía de un punto se transmite (idealmente) al siguiente. En las ondas circulares y esféricas estudiadas en este tema, en cambio, la energía que hace vibrar cada punto se reparte entre todos los que le rodean haciendo que la intensidad de los frentes de onda decrezca a medida que nos alejamos.

Un caso particular es el de las ondas planas (aquellas en las que el frente de ondas es plano). En ellas toda la energía que se propaga a través de una superficie sitúada a una distancia r₁ del foco se transmite a otra superficie situada a una distancia r₂, por lo que no existe tampoco (idealmente) atenuación.

Podemos cuantificar la atenuación que se produce en las ondas suponiendo dos frentes de onda esféricos a distancias r₁ y r₂ del foco respectivamente. Sabiendo que la superficie de una esfera viene dada por S=4·π·r², la intensidad de cada uno de ellos será:

$$I_1=\frac{E}{4·\mathrm{\pi }·{r_1}^2·t}=\frac{P}{4·\mathrm{\pi }·{r_1}^2}; I_2=\frac{E}{4·\mathrm{\pi }·{r_2}^2·t}=\frac{P}{4·\mathrm{\pi }·{r_2}^2}$$

La relación entre ellas se obtiene dividiendo una entre la otra y dandonos una medida para caracterizar el fenómeno de la atenuación:

Además, dado que la intensidad de un punto cualquiera cumple que I=cte·f²·A² y que la frecuencia f se mantiene constante, podemos escribir:

$$\boxed{\frac{I_1}{I_2}=\frac{{r_2}^2}{{r_1}^2}=\frac{{A_1}^2}{{A_2}^2}}$$

Absorción

Para entender la absorción te proponemos continuar con el experimento del comienzo del apartado. Sitúa, junto al recipiente con agua otro recipiente con gran cantidad de aceite. Si dejas caer dos canicas, una sobre cada recipiente, pero ambas desde igual altura, comprobarás que las ondas sobre el recipiente de aceite se amortiguan antes, a una distancia menor del foco. La razón es que, junto con el fenómeno de la atenuación, convive el de la absorción, que hace que parte de la energía del foco se gaste en fenómenos disipativos de las propias partículas del medio. Y estos son mayores en el caso del aceite, debido a la mayor viscosidad de este.

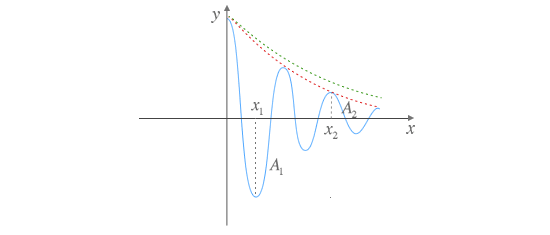
Absorción

A medida que nos alejamos del foco la amplitud de la onda disminuye de forma más pronunciada a lo que predice la atenuación. En la figura aparece representado en rojo la línea que une los valores de elongación máxima real que alcanza la onda según su distancia al foco. En verde se representa el valor teoríco que se alcanzaría si atendiéramos exclusivamente a los efectos de la atenuación. La diferencia entre el valor real y el valor esperado se explica por el fenómeno de la absorción.

La causa principal de la absorción, en el caso de las ondas mecánicas, es el rozamiento que hace que la energía mecánica se transforme en calor. En el caso de las ondas electromagnéticas la absorción se produce cuando la onda interacciona con la materia.

A diferencia de lo que ocurre con la atenuación, la absorción si que ocurre en ondas planas (también en las ondas unidimensionales). Por ello vamos a usar ondas planas para tratar de encontrar una ley que nos permita describir, de manera aislada, los efectos de la absorción. En nuestro estudio nos valemos de la siguiente imagen.

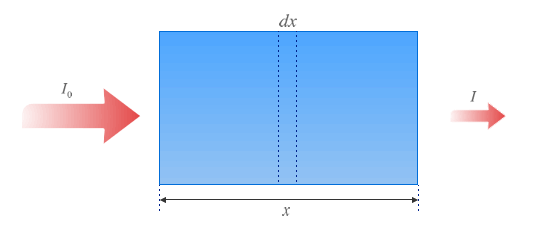
Absorción

Cuando una onda de intensidad I₀ llega a un medio absorbente de espesor x saldrá con una intensidad menor I de él.

Se puede comprobar experimentalmente que la disminución de intensidad dI que tiene lugar en un trozo diferencial del material dx se rige por:

$$dI=-\beta ·I·dx$$

Donde β es el llamado coeficiente de absorción. A partir de aquí, podemos agrupar…

$$dI=-\beta ·I·dx\Rightarrow \frac{dI}{I}=-\beta ·dx$$

...e integrar para obtener una expresión que rija la absorción. Los límtes de integración se deducen sabiendo que el inferior hace corresponder la intensidad inicial I₀ con un valor x=0 y que el superior hace corresponder una intensidad final I con un grosor final x⇒(I_{0, 0),(I,x) :}

$$\begin{gathered} {\int }_{I_0}^I\frac{dI}{I}={\int }_0^x-\beta ·dx\Rightarrow {\left[\ln \left(I\right)\right]}_{I_0}^I={\left[-\beta ·x\right]}_0^x\Rightarrow \ln \left(I\right)-\ln \left(I_0\right)=-\beta ·x\Rightarrow \\ \Rightarrow \ln \left(\frac{I}{I_0}\right)=-\beta ·x\Rightarrow e^{ln\left(\frac{I}{I_0}\right)}=e^{-\beta ·x}\Rightarrow I=I_0·e^{-\beta ·x} \end{gathered}$$ 

Espesor de semiabsorción

Se trata de otro parámetro usado para medir la absorción del material. Se define como el espesor necesario para reducir la intensidad de la onda incidente a la mitad de su valor original. Es decir, cuando:

$$x=D_{1/2}\Rightarrow I=\frac{I_0}{2}\Rightarrow \frac{I_0}{2}=I_0·e^{-\beta ·D_{1/2}}\Rightarrow \boxed{D_{1/2}=\frac{\ln \left(2\right)}{\beta }}$$

Observa que el espesor de semiabsorción no depende de la intensidad de onda incidente, sino que es un parámetro propio de cada material.

La siguiente gráfica recoge la variación de la intensidad de la onda plana de nuestro estudio a medida que atraviesa un medio, debida a los efectos de la absorción, y su relación con el coeficiente de semiabsorción.

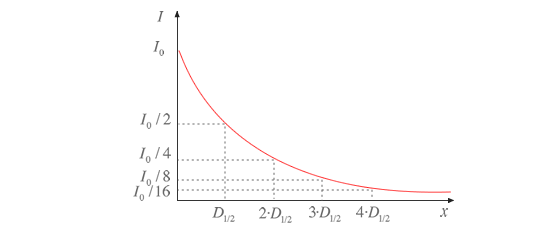
Espesor de semiabsorción

La gráfica de la figura representa la intensidad I de una onda plana de intensidad inicial I₀ a medida que se adentra una distancia x en un determinado medio absorbente.