Ondas Estacionarias

Hasta ahora hemos supuesto que las ondas se propagaban sin encontrar ningún obstáculo en su camino, en medios sin límites. Es lo que llamábamos ondas viajeras. Sin embargo, hay casos en los que la propagación se produce en medios cerrados, produciéndose reflexiones en los extremos del mismo que se superponen unas a otras. Estas superposiciones, que no son más que un caso particular de interferencias de ondas, pueden dar lugar a ondas estacionarias y tienen un perfil y unas características muy particulares que vamos a estudiar en este apartado a través de:

• El concepto de onda estacionaria
• Su fórmula
• Los nodos y los vientres de la onda, y la implicación que tiene su existencia para la propagación energética
• El ejemplo de ondas estacionarias en una cuerda fija por ambos extremos

¿Empezamos?

Concepto de onda estacionaria

Para entender las ondas estacionarias, nos centraremos en el caso de la suma de una onda armónica transversal con su reflejada. Esto implica que ambas contarán con igual amplitud, frecuencia y longitud de onda, pero sentido contrario.

Medios abiertos y cerrados

No todos los medios de propagación son capaces de producir, de manera natural, ondas estacionarias.

Decimos que un medio es abierto cuando la propagación no encuentra ningún obstáculo que refleje las ondas hacia el foco emisor. En ellos, la energía avanza en un único sentido. Ya habíamos dicho, cuando estudiábamos los tipos de ondas, que las ondas viajeras se daban en medios abiertos. ¿Eres capaz de adivinar qué medios producirán ondas estacionarias?

Efectivamente, se trata de los medios cerrados. Observa la siguiente imagen que te aclarará estos conceptos.

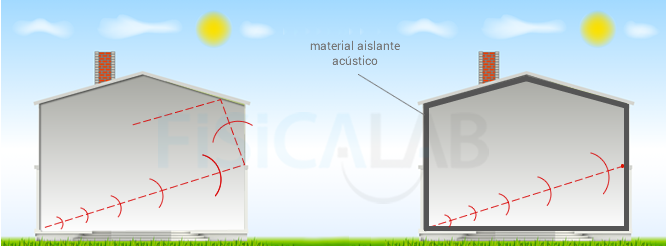
Medios abiertos y cerrados 

Si se produce un sonido en el interior de una habitación, tendremos que el techo, las paredes y el suelo reflejan parte de las ondas emitidas y las devuelven hacia el foco. El aire de la habitación, por tanto, es un medio cerrado para la onda sonora, y se podrían producir ondas estacionarias. Observa, sin embargo, que si recubrimos las paredes, techo y suelo con material absorbente, no se producirían las reflexiones y en ese caso el aire de la habitación si se consideraría medio abierto, haciendo imposible la aparición de ondas estacionarias.

Existen otros muchos medios capaces de producir ondas estacionarias, como, por ejemplo, una cuerda fija por ambos extremos o los tubos de cualquier instrumento de viento.

Ecuación de la onda estacionaria

Como dijimos, nos centraremos en el caso de que las ondas incidente y reflejada cuentan con igual amplitud, frecuencia y longitud de onda, pero sentido contrario.

Comprobación

Sean las ondas:

$$\left.\begin{array}{r}{y}_1=A·\sin \left(k·x-\omega ·t\right)\\ y_2=A·sin\left(k·x+\omega ·t\right)\end{array}\right\}y=y_1+y_2=A·\left(sin\left(k·x-\omega ·t\right)+sin\left(k·x+\omega ·t\right)\right)$$ 

Ahora, aplicando que $\sin \left(A\right)+\sin \left(B\right)=2·\cos \left(\frac{A-B}{2}\right)·sin\left(\frac{A+B}{2}\right)$ , y recordando que $\cos \left(-A\right)=\cos \left(A\right)$ , nos queda:

$$\begin{gathered} y=y_1+y_2=A·\left(sin\left(k·x-\omega ·t\right)+sin\left(k·x+\omega ·t\right)\right)=2·A·\sin \left(\frac{\left(k·x-\omega ·t\right)+\left(k·x+\omega ·t\right)}{2}\right)·\cos \left(\frac{\left(k·x-\omega ·t\right)-\left(k·x+\omega ·t\right)}{2}\right)= \\ =2·A·\sin \left(k·x\right)·\cos \left(\omega ·t\right)=\underset{A_T}{\underbrace{2·A·\sin \left(\frac{2·\pi }{\lambda }·x\right)}}·\cos \left(\omega ·t\right) \end{gathered}$$

Que es justamente lo que queríamos comprobar.

Formas alternativas

La expresión anterior es sólo una de las múltiples que podemos utilizar para describir una onda estacionaria. Podríamos, por ejemplo, tener las ondas originales en forma de coseno, en lugar de seno o podría existir inversión de fase en la reflexión ( una inversión en el sentido de vibración que se traduce en un cambio de fase de π radianes en la onda reflejada). El resultado al que llegaríamos tendría una forma distinta, aunque el significado físico sea similar.

Apuntaremos aquí también el resultado que se obtiene cuando, en lugar de partir de las ondas señaladas, partimos de dos ondas con formas:$y_1=A·\sin \left(\omega ·t-k·x\right) ; y_2=A·sin\left(\omega ·t+k·x\right)$ . La ecuación de la onda estacionaria quedará, mediante un desarrollo similar:

$$y=2·A·\cos \left(k·x\right)·\sin \left(\omega ·t\right)$$

En este caso, la onda estacionaria resultante presenta un máximo en x=0 dado que el coseno vale 1. En el anterior, la onda presentaba un mínimo. En general, la onda presentará un máximo o un mínimo en el medio en el que se refleja según las condiciones de contorno que imponga el mismo.

Experimenta y Aprende

Cargando...

Ondas estacionarias

La representación gráfica de las ondas incidente y reflejada nos permite entender claramente el aspecto de una onda estacionaria, su evolución con el paso del tiempo y la posición de sus vientres y nodos. Pulsa sobre el botón play para comenzar a experimentar.

La conclusión que debes extraer de todo esto es que, a la hora de resolver un ejercicio concreto, debes aprender y aplicar el desarrollo realizado antes que intentar utilizar unas fórmulas que podría llevarte a error.

Nodos y vientres

Como hemos apuntado, la elongación y de la ecuación de la onda estacionaria depende, entre otras, de la variable x, la posición, y esta se encuentra en el interior de un seno (o de un coseno). Esto implica que:

• Habrá puntos cuya elongación sea mínima (0). Llamaremos a estos puntos nodos. En ellos se cumplirá que:

  $$\sin \left(k·x\right)=\sin \left(\frac{2·\pi }{\lambda }·x\right)=0\Rightarrow \frac{2·\pi }{\lambda }·x=n·\mathrm{\pi }\Rightarrow \boxed{x=n·\frac{\lambda }{2}}$$

• Habrá puntos de elongación máxima (2·A). Los llamaremos vientres o antinodos. En ellos se cumplirá que:

  $$\sin \left(k·x\right)=\sin \left(\frac{2·\pi }{\lambda }·x\right)=\pm 1\Rightarrow \frac{2·\pi }{\lambda }·x=\left(2·n+1\right)·\frac{\mathrm{\pi }}{2}\Rightarrow \boxed{x=\left(2·n+1\right)·\frac{\lambda }{4}}$$

Siendo n= 0, 1, 2, 3..., en cualquiera de los casos anteriores.

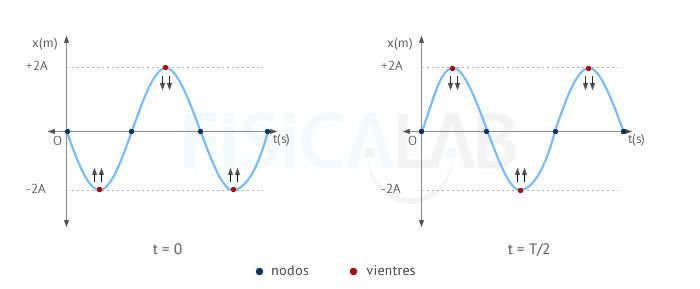
Nodos y Vientres 

La onda de la figura representa una onda estacionaria en dos instantes de tiempo concretos. Los puntos marcados en azul oscuro son los nodos de la misma. Los puntos cuya amplitud es 2·A y -2·A , marcados en rojo, son los vientres. Cada punto de la cuerda vibra según un m.a.s. cuya amplitud depende de su posición según: $A_T=2·A\sin \left(\frac{2·\pi }{\lambda }·x\right)$ . Hemos marcado el sentido de algunos de los puntos de la cuerda mediante las flechas negras.

Formas alternativas

Una vez más, si en lugar de considerar la ecuación de onda estacionaria cuya amplitud depende del seno, consideramos la del coseno $y=2·A·\cos \left(k·x\right)·\sin \left(\omega ·t\right)$, obtenemos:

• Posición de los nodos: $x=\left(2·n+1\right)·\frac{\lambda }{4}$ 
• Posición de los vientres: $x=n·\frac{\lambda }{2}$ 

Recuerda, no obstante, que la mejor manera de proceder para determinar la posición de nodos y vientres es hacer el desarrollo completo como has visto anteriormente y no emplear directamente fórmulas que podrían inducirte a errores.

Distancias entre nodos y vientres

Podemos calcular la distancia entre dos nodos restando las posiciones de dos consecutivos:

$$x_2-x_1=2·\frac{\lambda }{2}-1·\frac{\lambda }{2}=\frac{\lambda }{2}$$ 

A su vez, podemos calcular la distancia entre dos vientres restando las posiciones de dos consecutivos:

$$x_2-x_1=\left(2·2+1\right)·\frac{\lambda }{4}-\left(2·1+1\right)·\frac{\lambda }{4}=\frac{\lambda }{2}$$

Observa que, los resultados finales son los mismos que si hubiésemos considerado la onda original con una amplitud resultante en función del coseno.

Consideraciones energéticas

Observa que la existencia de nodos implica que en una onda estacionaria, a diferencia de lo que ocurría en las viajeras, no se propaga energía a lo largo de la misma, pues esta no puede atravesar los nodos, en reposo permanente. De hecho, en sentido estricto, una onda estacionaria no es un movimiento ondulatorio (recordemos, aquel caracterizado por la propagación de energía sin propagación de materia) y la única razón por la que la consideramos una onda es que es la superposición de dos ondas viajando en sentido contrario.

Cuerda fija por ambos extremos

Un caso especialmente interesante de ondas estacionarias se da cuando excitamos a una determinada frecuencia una cuerdas fija por ambos extremos. No todas las frecuencias de excitación van a producir ondas estacionarias. Veámoslo.

Empezamos considerando una cuerda de longitud L. Al estar fijos ambos extremos, los puntos x=0 y x=L han de ser nodos de la onda estacionaria (tener elongación 0 en todo momento). Dicho de otro modo, las condiciones de contorno serán:

$$y(0,t)=0 ;\hspace{0.17em}y(L,t)=0$$

Instrumentos de cuerda 

Los instrumentos de cuerda como la guitarra, el piano, o el violín son ejemplos de lo que ocurren cuando se generan ondas estacionarias en cuerdas fijas por los dos extremos.

Sabemos que los nodos se encuentran separados media longitud de onda y, por tanto, en la onda estacionaria que se genere debe haber un número entero de semilongitudes de onda que se ajuste a la longitud L de la cuerda según: $n·\frac{\lambda }{2}=L (n=1, 2, 3...)$  Si renombramos λ como λ_n,y la despejamos de la expresión anterior, podemos escribir:

Por tanto, las longitudes de onda quedan "cuantizadas", es decir, sólo son posibles aquellas que cumplan la relación que marca la expresión anterior:${\lambda }_1=2·L\hspace{0.17em}, {\lambda }_1=L , {\lambda }_3=\frac{2·L}{3}$ , etc.

Por otro lado, esta "restricción" se extiende igualmente a las frecuencias posibles. Efectivamente, la frecuencia de una onda y su longitud de onda se relacionan a través de la expresión de la velocidad de fase v y, dado que esta sólo depende del medio, podemos escribir $v=\lambda ·f\Rightarrow f_n=\frac{v}{{\lambda }_n}=n·\left(\frac{v}{2·L}\right)$ 

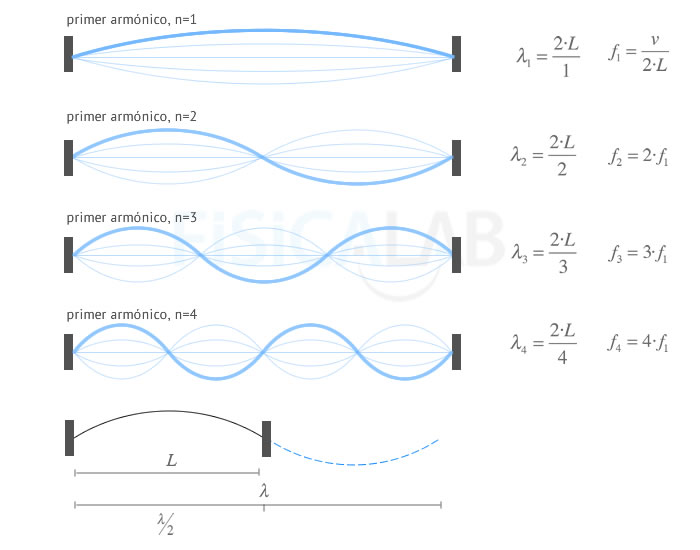
Armónicos en cuerda fija por ambos extremos

Cuando provocamos una oscilación en una cuerda fija por ambos extremos pueden aparecer ondas estacionarias si la excitamos con la frecuencia adecuada. En la figura se representan distintos valores de frecuencia que dan lugar a los primeros 4 armónicos. En todos ellos se cumple que λ_n = 2·L/n.  Observa que al armónico n corresponde una onda estacionaria con n vientres y n+1 nodos.